© 2010  Rasmus ehf    og Jóhann Ísak

Vektorer 

Introduksjon 1. 

Addisjon og subtraksjon av vektorer. Multiplikasjon av vektorer og konstanter.

 

Størrelser som temperatur og lengde kan beskrives med tallverdier. Disse kalles skalarverdier. For størrelser som akselerasjon og kraft, må vi også ha med retningen. Slike størrelser kalles vektorer. Vektorer er ikke nødvendigvis faste i forhold til rommet. For eksempel, å flytte seg 5 meter nord på et horisontalt plan, skjer på samme måte uansett hvor i planet det skjer.
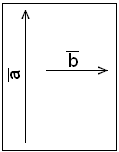
Vektorer kan tegnes som piler. Lengden på en pilen viser størrelsen, og retningen på pilen viser vektorens retning. En forflytning på 5 m nordover, kan for eksempel skrives som en 5 cm lang, loddrett pil som peker oppover. En forflytning på 2 m østover kan vises som en 2 cm lang, vannrett pil til høyre.

En vektor er en størrelse med retning, og tegnes som en pil.
Pilens lengde er vektorens størrelse, og retningen er vektorens retning. 

Vektorer kan skrives som en liten bokstav med strek over, eller med en strek over punktene hvor vektoren starter og slutter (for eksempel   hvis vektoren går fra punkt A til punkt B.

På bildet under ser vi at pilene AE, FK og DH har samme lengde og retning. Pilene er like, og de symboliserer samme vektor, vektor  . Om vi tegner inn pilene BF, CG, EJ, GL og HM, kan alle betegnes som vektor .

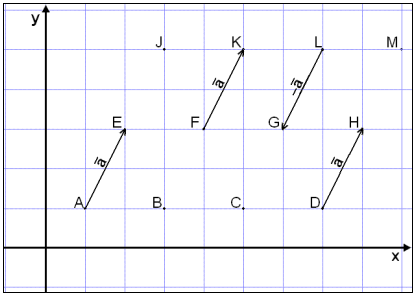
På bildet over ser vi at pilen LG er parallell med pilen FK, men har motsatt retning. Vi kan derfor si at pilen LG betegner vektoren − .

Her er flere muligheter.

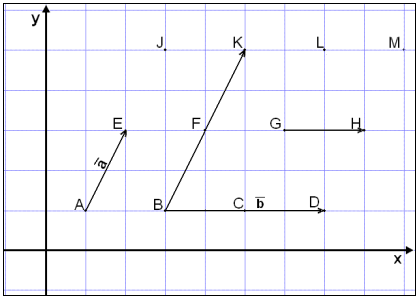
Hvis pilen AE betegner vektoren , må en dobbelt så lang pil, pilen BK, betegne vektoren 2.
På samme måte kan vi si at hvis pilen BD betegner vektoren , må pilen GH betegne ½∙  , fordi den er halvparten så lang som BD.

På bildet under har vi satt sammen to vektorer som begge betegner vektoren  .

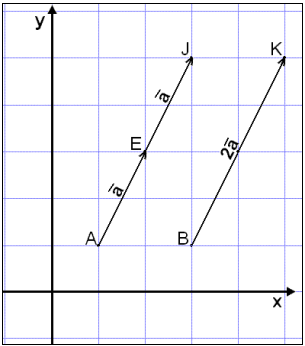
Av det vi ser på bildet, kan vi trekke slutningen at   +  er lik 2.  Addisjon av vektorer er altså det samme som å koble sammen vektorenes startpunkt og endepunkt.

 

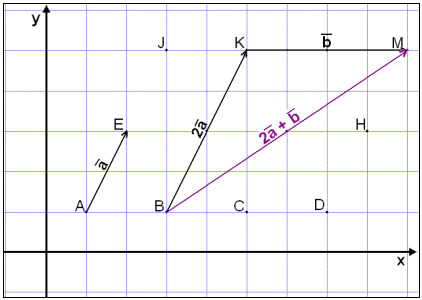
På bildet over representerer pilen AE vektoren  , og pilen KM representerer vektoren  . Pilen BK er parallell med AE, men dobbelt så lang. Hvis vi kobler sammen BK (2) og KM (), får vi vektoren 2 + , som representeres av pilen BM.

 

 

Eksempel 1

På bildet under representerer pilen AE vektoren , AC vektoren  og AM vektoren  .

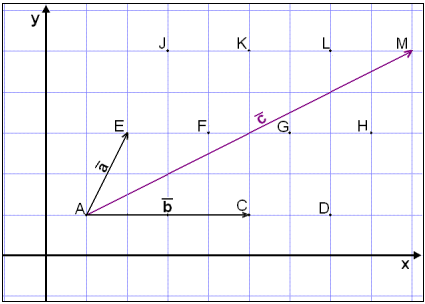
Hvordan kan vi skrive vektoren    ved hjelp av vektorene   og ? 
Vi multipliserer vektoren  med 2
(legger pilen EJ till AE) og legger til 1½ .
 (Se bildet)

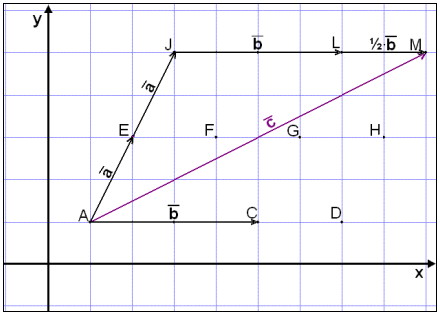
Vi får at   = 2  + 1½ .

Det vi har gjort, er å finne komponentene til vektoren   ved hjelp av vektorene  og . Komponentene er 2 og 1½ .

Eksempel 2

Vi bruker de samme vektorene og koordinatene som i eksempel 1, og finner en pil som tilsvarer vektoren  − .

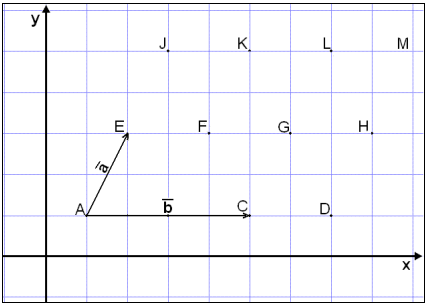
Vi begynner med å konstatere at  −  er den samme vektoren som   + (− ). Vi tegner vektoren fra punkt G til punkt L. Så legger vi til en pil som er like lang som vektor , men har motsatt retning. Resultatet blir vektoren .

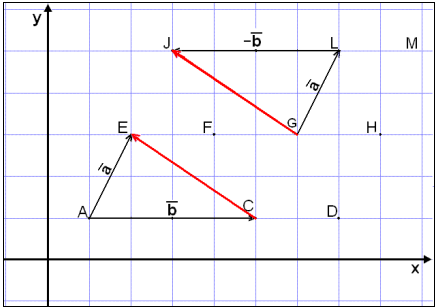
Vi ser av bildet over at differensen mellom    og  er  (samme vektor som ).
Det gir oss en måte å finne differensen mellom to vektorer.

Differensen mellom vektorene  og  kan finnes ved å snu vektoren , og koble den til enden av  .

  og  kan også tegnes ut fra samme punkt.  −  blir da vektoren som går fra enden av til enden av  .

Siden vektorer består av både lengde og retning (vinkel), må vi ofte bruke trigonometri for å løse vektorproblemer. Dette kan for eksempel være å finne lengden eller retningen til en vektor. Det er vanlig å bruke absoluttverdier når man skriver lengden av en vektor.

Lengden av vektoren  skrives | |

Eksempel 3

I byggebransjen er det viktig å regne ut effekten av alle kreftenes samspill på de forskjellige delene av en bygning. Vi tenker oss at kreftene som vi ser på bildet under alle virker på samme objekt, og skal regne ut den samlede kraften (resultantkraften).

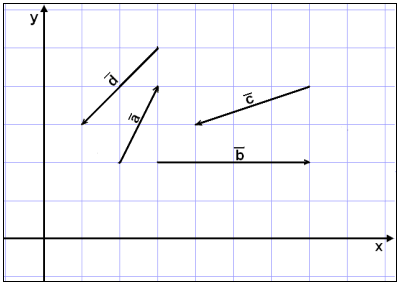
Vi finner summen av vektorene ved å koble dem sammen.

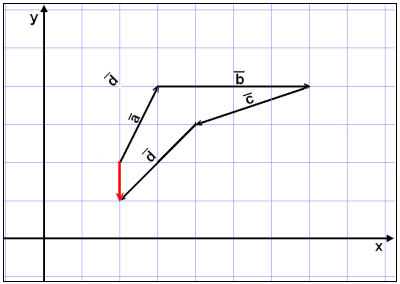
De sammenkoblede vektorene slutter en rute nedenfor startpunktet. Det betyr at kreftenes samlede effekt er å dra objektet en rute ned.

Eksempel 4

Vi bruker samme vektorer som i eksempel 3, og regner ut  −  −  + .

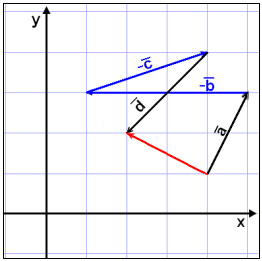Vi snur vektorene * og , og kobler sammen alle vektorene.

 

Resultatet er den røde vektoren på bildet, som går fra startpunktet til endepunktet til de sammenkoblede vektorene. Vi flyttet vektoren   for å kunne utnytte koordinatsystemet bedre. Posisjonen i planet eller rommet er som vi vet likegyldig. Koordinatsystemet er ikke nødvendig, men det gjør det lettere å tegne og lese av verdiene til vektorene.

Eksempel 5

Et skip seiler i nordover med en fart på 24 sjømil i timen (24 knop). En sterk strøm på 7 knop driver skipet østover. Det vil si at når skipet har seilt 24 sjømil mot nord, har det drevet 7 sjømil mot øst. Vi skal regne ut skipets virkelige fart og retning i forhold til havbunnen.

Vi tegner opp som to vektorer, og legger dem sammen. Farten tilsvarer  | |, og retningen er vinkel A.

 

| | kan vi regne ut ved hjelp av Pythagoras.

   | |2 = 242 + 72

              = 576 + 49 = 625

    | | =

              = 25 sjømil/time.

 

Vi regner ut vinkelen A slik:

    tan A = motstående side / nærliggende side

              = 7/24

           A = tan −1(7/24) ≈ 16°

Eksempel 6

En ferge må seile over en 100 m bred elv. Fergens fart er 3 m/s og vannet renner nedover elven i 1 m/s.

a)   Hvor lang tid bruker fergen på å seile rett over elven?

      Her har ikke strømmen noe å si, fordi fergen ikke jobber mot den. Vi trenger bare å regne ut hvor lang tid det tar å seile 100 m med en fart på 3 m/s.

        

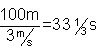
b)   Nå regner vi ut fergens virkelige fart.

Vi tegner opp vektorene som viser både båtens og elvens fart og retning.

Her kan vi bruke Pythagoras.

   x2 = 32 + 12 = 9 + 1 = 10

 x = 10  3,2 m/s

    

c)   Hvor langt nedover driver båten før den er over elven?

I trekanten under er hypotenusen den veien fergen må seile, og den lengste kateten viser korteste vei over elven (100 m). Den korteste kateten, x, viser strekningen som fergen har drevet ned elven.

Trekanten på bildet over er proporsjonal med trekanten som dannes av vektorene i b).

   1/3 = x/100 Vi ganger begge sider med 100.

      x = 100/ 3 = 33⅓ m

Vi har løst problemet ved hjelp av vektorer, men kunne også ha løst det geometrisk. Vi vet at elven renner 1 m/s, og at det tar 33⅓ s for fergen å krysse elven. Dermed vet vi at fergen driver 33⅓ m nedover elven. Nå som vi også har regnet ut problemet på den vanskelige måten, ser vi sammenhengen mellom vektorutregninger og trekanter.

d)  

Fergen skal ta den korteste veien over elven, og havne nøyaktig på motsatt side av elven. Den må derfor seile oppover elven med vinkelen y°. Hvor stor må vinkelen y°  være for at fergen skal kunne motvirke strømmen, og havne på nøyaktig motsatt side av elven?

Vi vet at fergen driver 1 m nedover for hver tredje meter den seiler. Dette vises av trekanten på bildet under, og vi må regne ut vinkelen y°.

         y° = sin−1(1/3) 19,5°

e)  

Hvilken fart har fergen om den seiler oppover som i d)?

Nå seiler fergen oppover i vinkelen 19,5°. Fergens fart og elvens strøm er den samme som før, men vi vil finne x.

Vi bruker Pythagoras til å finne summen av vektorene.

   x2 + 12 = 32

           x2 = 9 − 1 = 8

            x = 8 2,8 m/s

Eksempel 7

To tau er festet foran i midten av en tung slede, og hvert tau drar sleden med en kraft på 100 N. Vinkelen mellom tauene er 60°. Vi skal regne ut størrelsen på den samlede kraften som drar sleden fremover. Først tegner vi en tegning.

Vi bruker først vektoraddisjon, og deretter trigonometriske regler.

 

Vektoren x, som vi skal finne, deler vinkelen på 60° i to like vinkler. Dette gir oss en likebeint trekant med to vinkler på 30° , og en vinkel på120°. Nå skal vi bruke sinussetningen til å regne ut x.

 

 

Se på eksemplene, og regn deg gjennom test 1 i Vektorer.

Husk å fylle ut sjekklisten underveis.