© 2008  Rasmus ehf    og Jóhann Ísak

Trigonometriske formler

Introduksjon 2  

Formlene for sinus, cosinus og tangens til summen eller differensen til to vinkler, er ofte veldige nyttige. Nå skal vi bevise noen av formlene.

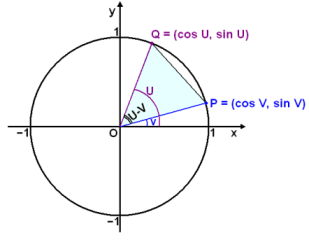
Trekanten OPQ i figuren har hjørnene P, Q og O, som er sentrum i koordinatsystemet. Vi kaller vinkelen mellom x-aksen og OQ for u, og vinkelen ellom x-aksen og OP for v. Vinkel POQ er derfor u – v. Punktet Q har koordinatene (cos u, sin u), og punktet P har koordinatene (cos v, sin v). Avstanden mellom P og Q kan skrives |PQ|, og vi skal nå finne den ved hjelp av avstandsformelen.

   |PQ|2 = (cos u − cos v)2 + (sin u − sin v)2  

            = cos2u − 2 cos u cos v + cos2v

               + sin2u − 2 sin u sin v + sin2v  

            = 1 − 2 cos u cos v− 2 sin u sin v + 1

            = 2 − 2 cos u cos v − 2 sin u sin v

(avstand)2 = (x2−x1)2 + (y2−y1)2 Gang ut parentesene og forenkle.  

Vi finner |PQ| ved hjelp av cosinusregelen.

   |PQ|2 = 12 + 12 − 2∙1∙1∙cos (u − v)

             = 2 − 2∙cos (u − v)

Vi setter de to uttrykkene lik hverandre, og får:

       2 − 2∙cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v

     − 2∙cos (u − v) = − 2 cos u cos v − 2 sin u sin v

Hvis vi deler alle ledd på −2, får vi denne formelen:

cos (u − v) = (cos u cos v) + (sin u sin v)

Vi får en annen formel ved å sette inn –v i formelen istedenfor v.

   cos (u − (−v)) = cos u cos (−v) + sin u sin (−v)

Ved hjelp av reglene fra enhetssirkelen, (−v) = cos v and sin (−v) = − sin v kan vi skrive om uttrykket slik:

cos (u + v) = (cos u cos v) − (sin u sin v)

I figuren under har vi tegnet to trekanter. Den ene har vinkelen v mellom hypotenusen og x-aksen, den andre har samme vinkel mellom hypotenusen og y-aksen. Dette må bety at trekantene er helt like.

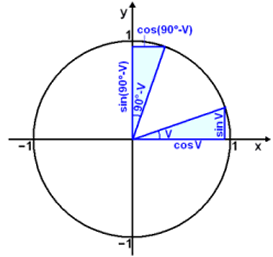
Det gir oss følgende regler:

   cos v  = sin (90° − v)    og   sin v = cos (90° − v)

Nå setter vi inn 90° istedenfor u og (u + v) istedenfor v, og får to regler for sinus:

    sin (u + v) = cos (90° − (u + v))

                     = cos ((90° − u) − v)

                     = cos (90° − u) cos v + sin (90° − u) sin v

                     = (sin u cos v) + (cos u sin v)

Vi har funnet formelen for sin (u + v):

sin (u+v) = sin u cos v + cos u sin v

Hvis vi nå setter inn (−v) for v i formelen, får vi dette:

sin (u − v) = sin (u + (−v))

                    = sin u cos (−v) + cos u sin (−v)

                    = sin u cos v − cos u sin v

 Vi bruker formelen

cos(u−v) = (cos u cos v)−(sin u sin v)

og sin v = cos (90° − v) og cos v  = sin (90° − v).

Vi har funnet formelen for sin (u − v):

sin (u-v) = sin u cos v - cos u sin v

Ved å sette inn v for u i formlene (u + v) og cos (u + v) får vi formlene for doble vinkler, sin (u + u) og cos (u + u).

sin 2u = 2 sin u cos u

cos 2u = cos2 u − sin2
Formelen for cos 2u kan skrives på to andre måter, ved hjelp av formelen cos 2 u + sin 2 u = 1. 

Først erstatter vi cos 2 u ved å bruke cos 2 u = 1 − sin 2 u og deretter sin 2 u ved hjelp av sin 2 u = 1 − cos 2 u. Vi får formlene:

cos 2u = 2 cos2 u − 1

cos 2u = 1 − 2 sin2 u

Eksempel 1

Bruk formlene over til å finne eksakte verdier av sin 15°og cos 15°.

Vi vet allerede at cos 45° = 2/2, sin 45° = 2/2, cos 60° = ½ og sin 60° = 3/2.

Vi bruker formelen for cos (u - v):

   cos 15° = cos (60° − 45°)

                 = cos 60° cos 45° + sin 60° sin 45°

                 = ½∙2/2 + 3/2∙2/2

                 = 2/4 + 3∙2/4

                 = 2∙(1 + 3)/4

Vi bruker formelen for sin (u - v):

     sin 15° = sin (60° − 45°)

                 = sin 60° cos 45° − cos 60° sin 45°

                 = 3/2∙2/2 − ½∙2/2

                 = 3∙2/4 − 2/4

                 = 2∙(3 − 1)/4

Eksempel 2

Forenkle uttrykket sin (270° − v).

Vi bruker formelen sin (u − v) = (sin u cos v) − (cos u sin v).

sin (270° − v) = sin 270° cos v − cos 270° sin v

                       = −1∙ cos v − 0∙ sin v         

                       = − cos v

sin 270° = −1

 cos 270° = 0

Eksempel 3

Finn en formel for cos 3x that som bare består av sin x og cos x.

Vi bruker formelen cos (u + v) = cos u cos v − sin u sin v og erstatter u med 2x og v med x.

cos (2x + x) = cos 2x cos x − sin 2x sin x

cos 2x = cos2x − sin2x       sin 2x = 2 sin x cos x

                      = (cos2 x − sin2 x)∙cos x − (2 sin x cos x)∙sin x

                      = cos3 x − sin2 x cos x − 2 sin2 x cos x

                      = cos3 x − 3 sin2 x cos x

Eksempel 4

Løs likningen  sin 2x + 2 sin x = 0 , 0 x < 2.

              sin 2x + 2 sin x = 0

   2 sin x cos  x + 2 sin x = 0

         2 sin x (cos  x + 1) = 0

Bruk sin 2x = 2 sin x cos x

En løsning er sin x = 0

         x = 0 eða (0° eða 180°)

En annen løsning er cos x = −1

          x = p(180°)

Løsningene er derfor  0 og .   

Eksempel 5

Løs likningen  7 cos2 x + 5 sin2 x + 6 sin 2x = 0

Først bruker vi formelen  sin 2x = 2 sin x cos x.

   7 cos2 x + 5 sin2 x + 12 sin x cos x = 0

Denne typen likninger, med to faktorer av sin eller cos i hvert ledd, kan løses ved å dele alle ledd på cos2x, slik at vi får en tangenslikning.

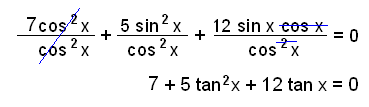
Dette er en kvadratisk likning med  a = 5, b = 12 og c = 7.

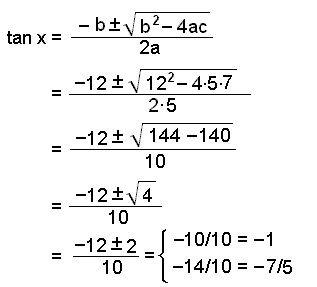
   tan x = −1 gefur x = −/4 + k∙  (−45° + k∙180°)

   tan x = −7/5 gir ikke en vinkel som kan uttrykkes eksakt ved hjelp av

         x ≈ −0,95 + k∙ (54,5° + k∙180°)

Prøv Test 2 i Trigonometri.

Husk å bruke sjekklisten.