© 2007  Rasmus ehf og Jóhann Ísak Pétursson

Mengdelære

Skriv ut

Introduksjon 2   Numeriske mengder

I matematikk finnes det flere forskjellige numeriske mengder (mengder av tall).

Her er et diagram som viser forholdet mellom dem.

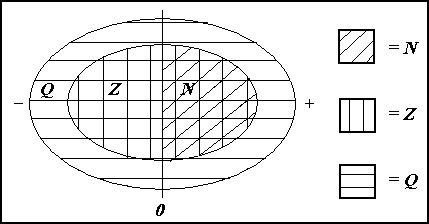
Den enkleste mengden er mengden av naturlige tall. Når man snakker om denne mengden, bruker man alltid bokstaven N. N = { 1,2,3,∙∙∙ }. De naturlige tallene er tallene man bruker når man teller, og de fortsetter i det uendelige. Man tar ofte med null i mengden av naturlige tall, men da må man skrive N₀, ikke N.  N₀ = { 0,1,2,3,∙∙∙ }.

Bokstaven Z brukes for å symbolisere mengden av hele tall. Disse kan være både positive og negative.  Z = { ∙∙−2,−1,0,1,2,∙∙ }.

Mengden N er en delmengde av mengden Z.

N    Z

Den tredje mengden som vi skal nevne skrives Q. Dette er mengden av alle rasjonelle tall, altså mengden av alle brøker som kan skrives med hele tall i teller og nevner. Legg merke til at alle hele tall også kan skrives som brøker, så både Z og N er delmengder av Q.

Z   Q og N Q

Legg merke til at alle elementene i disse tre mengdene kan skrives med hele tall.

Nå skal vi se på desimaltall.

Eksempel 1

Når vi regner ut 1 dividert med 3, får vi

0,333∙∙∙∙

og 4 dividert med 33 gir

0,1212∙∙∙∙

Desimaltallene i disse eksemplene har et uendelig antall desimaler etter komma. Den samme rekkefølgen av desimaler gjentar seg igjen og igjen. De kalles periodiske desimaler.

I det første eksempelet er perioden en desimal, tallet 3. I det andre eksempelet består perioden av to desimaler, hvor 1 og 2 gjentar seg. Alle rasjonelle tall kan skrives som periodiske desimaler.

Disse eksemplene viste hvordan en brøk kan forandres til et desimaltall ved divisjon. Nå skal vi se på hvordan et desimaltall kan forandres til en brøk.

Hvis desimaltallet har et bestemt antall desimaler, kan vi forandre det til en brøk ved å flytte kommaet til vi har et helt tall, og så dividere det med 10, 100, 1000... etter hvor mange plasser vi flyttet kommaet.

Eksempel 2

Skriv 0.3, 0.12 og 0.1212 som brøker.

0,3

=

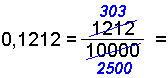Denne metoden virker ikke med periodiske desimaltall, fordi de har et uendelig antall desimaler etter komma. I sånne tilfeller må vi bruke en annen metode.

Eksempel 3

Gjør 0.333∙∙∙∙∙, 0.1212∙∙∙∙∙ og 1.14333∙∙∙ til brøker

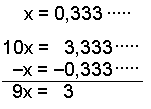		Kall tallet for x. Når perioden består av en desimal, ganger vi tallet med 10, så vi får 10x. Deretter trekker vi det første tallet fra 10x.  På denne måten blir vi kvitt alle desimalene.
		Til slutt dividerer vi svaret med 9 for å finne x. Forkort hvis det er mulig.

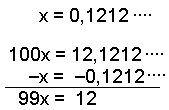		Kall tallet for x.  Denne gangen har perioden to desimaler, så vi multipliserer tallet med 100 og får 100x Deretter trekker vi det første tallet fra 100x.
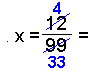
		Igjen blir alle desimalene borte Til slutt dividerer vi svaret med 99 for å finne x. For kort hvis det er mulig.

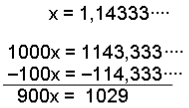		I dette eksemplet må vi begynne med å multiplisere med 100 slik at perioden starter rett etter komma Denne gangen har perioden bare en desimal, så vi multipliserer igjen med 10. Så trekker vi 100x fra 1000x, slik at desimalene blir borte.
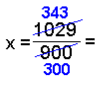		Til slutt dividerer og forkorter vi for å finne x.

Prøv test 2 i Mengdelære.
Husk å fylle inn resultatet i sjekklisten din.