© 2010 Rasmus ehf  og Jóhann Ísak

Funksjoner 2

Introduksjon 6

Inverse funksjoner

Vi har allerede sett at noen funksjoner har en omvendt funksjon, en invers. Funksjonene f(x) = x² og g(x) = √x  er inverse av hverandre hvis vi begrenser x - verdiene til ikke - negative tall. Disse funksjonene opphever hverandre. Hvis vi setter et tall inn i den ene funksjonen, og deretter setter verdien vi får inn i den andre, står vi igjen med det opprinnelige tallet. Her er et eksempel:

   f(x) = x² og g(x) =

   f(2) = 2² = 4 og g(4) = √4 = 2

   f(g(a)) = = a

   g(f(a)) =  = a

Det har ikke noe å si hvilken funksjon vi bruker først, resultatet blir det samme. Verdiområdet til den ene funksjonen blir definisjonsmengden til den andre.

En funksjon har en invers bare hvis den er en - til - en og surjektiv. I dette tilfellet begrenser vi x - verdiene til ikke - negative tall, slik at funksjonen       f(x) = x² oppfyller kravene. En funksjon har med andre ord en invers hvis den er strengt voksende eller avtakende i hele definisjonsområdet. Funksjonen g(x) = √x er strengt voksende, og kan bare ha ikke - negative x - verdier. Dette betyr at  f(x) = x²  også er begrenset til ikke - negative verdier.

For å finne likningen til en invers ved algebra, må vi løse likningen for x. Se på eksempelet.

Eksempel 1

Finn inversene til disse funksjonene:

a)   f(x) = 2x + 4

          y = 2x + 4                erstatt f(x) med y

      –2x = 4 – y

          x = –2 + ½y              Del alle ledd på  –2

      Dette er en likning hvor x er en funksjon av y. Navnet på variabelen har ingenting å si, så vi bytter om x og y. Hvis vi kaller funksjonen g, får vi likningen for den inverse av f(x).

g(x) = y = ½x – 2.

       Vi kan kontrollere ved å sette inn et tall.

          f(1) = 2·1 + 4 = 6 og g(6) = ½·6 – 2 = 3 – 2 = 1

      Hvis vi bruker den generelle verdien a, får vi:

         f(a) = 2a + 4  og  g(2a+4) = ½·(2a+4) – 2 = a + 2 – 2 = a

b)   f(x) = sin 2x,  D_f = [–/4,/4ñ , f(x) er strengt økende i intervallet, og har derfor en invers funksjon.

          y = sin 2x

        2x = sin^–1 y

          x = ½ sin^–1 y

      Den inverse funksjonen er g(x) = ½ sin^–1 x.

   I de fleste lærebøker skrives den inverse funksjonen med ^–1 slik at f(x) har den inverse funksjonen f ^–1(x).
Dette betyr ikke ¹/f, det er bare en måtte å betegne den inverse funksjonen.

      I eksempelet over er f ^–1(x) = ½ sin^–1 x.

      Kontroller.

         f(/12) = sin 2/12 = ½ 

         f ^–1(½) = ½·sin^–1 ½ = ½·/6 = /12

c)   f(x) = e^2x

          y = e^2x

      ln y = ln e^2x = 2x

          x = ½ ln y

      Den inverse av  f(x) er derfor  f ^–1(x) = ½ ln x.

d)   f(x) = x² – 1, D_f = R₊

          y = x² – 1

          x² = y + 1

Den inverse funksjonen er

   e) 

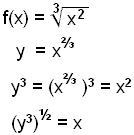Vi velger Df = R+ og opphøyer begge sider i tredje. Vi tar deretter kvadratroten av svaret.

       Den inverse funksjonen er  

Eksempel 2

Hvordan må vi begrense definisjonsmengden til funksjonen f(x) = sin x slik at den har en invers? Vi vet at en kontinuerlig funksjon som er strengt voksende eller avtakende, alltid har en invers.

Vi ser derfor på den deriverte av funksjonen f(x) = sin x , f´(x) = cos x.  

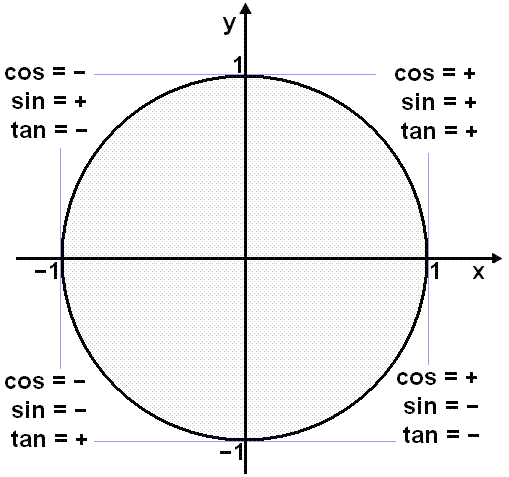
Vi ser av enhetssirkelen at cos x er positiv fra  –/2 to  /2 og negativ i resten av sirkelen.

Se på grafen til f(x) = sin x.

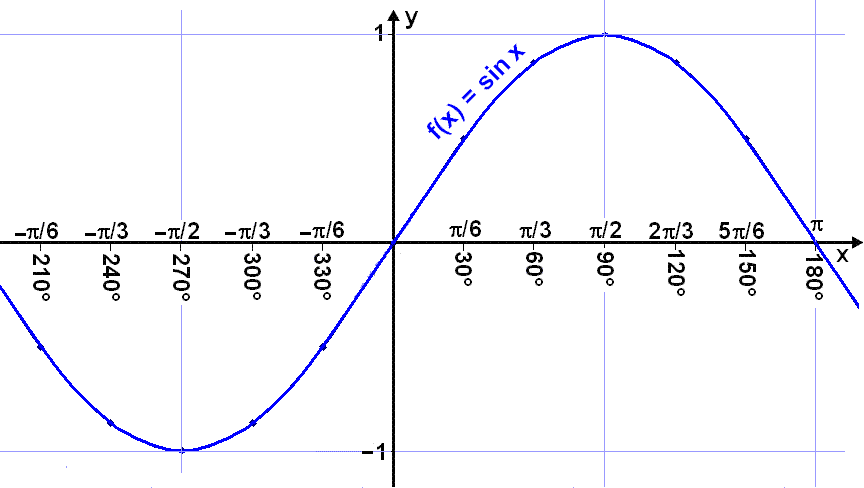
       Vi ser at grafen øker for –/2 < x < /2, så f(x) = sin x har en invers hvis vi begrenser definisjonsmengden til dette intervallet.
 Vi kunne ha valgt et annet intervall, som /2 < x < 3/2 hvor funksjonen er avtakende, men det er vanligere å velge intervallet –/2 < x < /2.

Eksempel 3

Finn intervallet hvor funksjonen f(x) = x² – 4x + 3 øker, begrens definisjonsmengden til dette intervallet, og finn formelen for den inverse funksjonen. Tegn til slutt grafene for både f(x) og f^–1(x)  i samme koordinatsystem.

Vi finner først det stasjonære punktet i parabelen ved å finne ut hvor den deriverte er null.

   f(x) = x² – 4x + 3

   f´(x) = 2x – 4 = 0

      2x = 4

        x = 2

Det stasjonære punktet er i x = 2, og funksjonen øker etter dette. Vi velger derfor definisjonsmengden

Df =

.

For å finne den inverse, må vi løse y = x² – 4x + 3 for  x.

Vi lager en verditabell, for å kunne tegne grafen.

Når vi regner ut f(2), ser vi at f(x) = y tar verdier fra  –1 og oppover (funksjonen er voksende). Vi begynner derfor med å finne f^–1(–1).

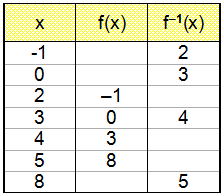
De to grafene vises under.

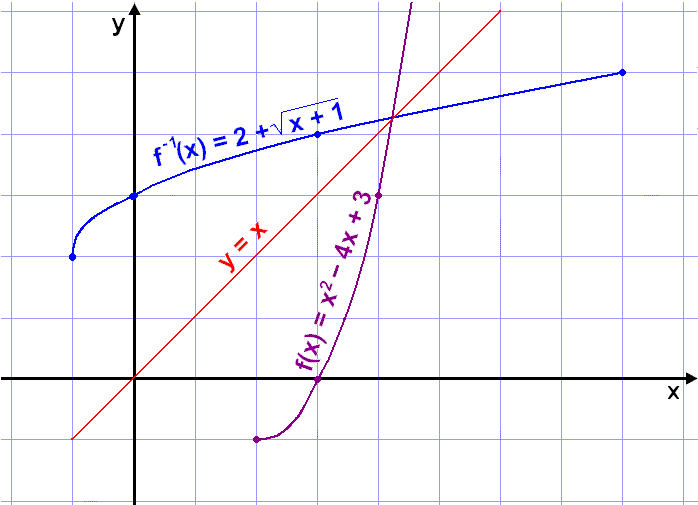
Vi ser at de to grafene speiler hverandre om linjen y = x. Dette kan vi også se i verditabellen. Hvert punkt på f(x) speiler et punkt på f ^–1(x). For eksempel er (2, –1)  på f(x), og (–1, 2)  på f ^–1(x).  (3, 0) er på f(x), og (0, 3) på f ^–1(x). Generelt kan vi si at hvis (a, b) er på den ene grafen, finner vi (b, a) på den inverse.

Eksempel 4

Se på funksjonen f(x) = e^x og den inverse funksjonen g(x) = ln x.

Funksjonen f(x) = e^x  gjelder for alle x - verdier, så definisjonsmengden er alle reelle tall (mengden R).
Verdiene som f(x) = e^x tar er alltid positive, så verdiområdet er intervallet .
Funksjonen  g(x) = ln x  er bare definert for positive x - verdier, så definisjonsmengden er .
På den annen side gjelder funksjonen g(x) = ln x for alle relle tall, så verdiområdet er R.

Verdiområdet til en funksjon er lik definisjonsmengden til den inverse funksjonen, og definisjonsmengden er lik verdiområdet til den inverse funksjonen.

Grafene til de to funksjonene er vist under. Legg merke til at de speiler hverandre om y = x.

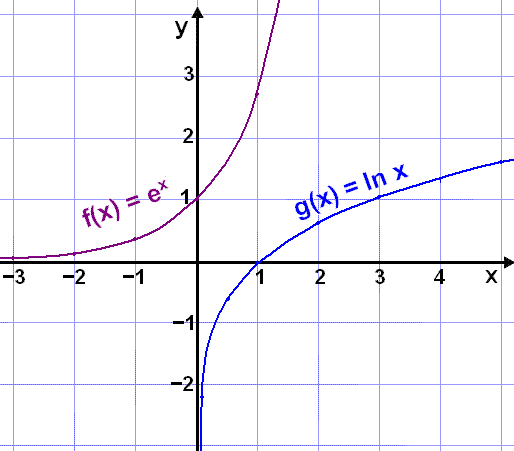
Eksempel 5

Finn intervallet hvor funksjonen øker. Finn den inverse funksjonen ved å velge dette intervallet som definisjonsmengde, og tegn grafene i samme koordinatsystem.

Deriver for å finne ut hvor funksjonen vokser og avtar.

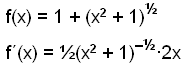
Nevneren er alltid positiv, så det er x i nevneren som forteller oss hvor funksjonen vokser og avtar.

Funksjonen vokser for positive verdier av x, så vi velger definisjonsområdet

Df =

Vi løser for x, og finner inversen.

             y = 1 + (x² + 1)^½

       y – 1 = (x² + 1)^½

   (y – 1)² = x² + 1

            x² = (y – 1)² – 1

                = y² – 2y + 1 – 1

                = y² – 2y

( vi velger den positive verdien for x )

Den inverse funksjonen er

Grafene til f(x), f ^–1(x) og linjen  y = x ser slik ut:

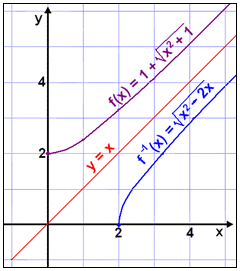
Eksempel 6

Finn den inverse av funksjonen  og tegn grafene i samme koordinatsystem.

Grafen har en vertikal asymptote  x = 1 og en horisontal asymptote y = 2. Definisjonsmengden inneholder ikke x = 1.

Vi deriverer for å finne stigningstallet til grafen.

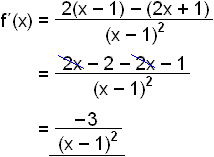
Nevneren er alltid positiv, og telleren alltid negativ. Det betyr at grafen alltid har negativt stigningstall. Funksjonen avtar altså i hele definisjonsområdet.

Vi finner den inverse funksjonen ved å løse for x.  

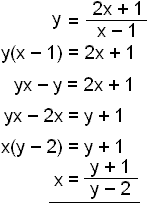
Den inverse er

Bli kvitt brøken, og flytt alle ledd med x til venstre side. Flytt alt annet til høyre side. Vi ser at y ikke kan være 2.

Funksjonen har en vertikal asymptote i x = 2, og en horisontal asymptote i y = 1. Dette er det motsatte av f(x), som har en vertikal asymptote i x = 1 og en horisontal asymptote i y = 2.

Se på de to grafene.

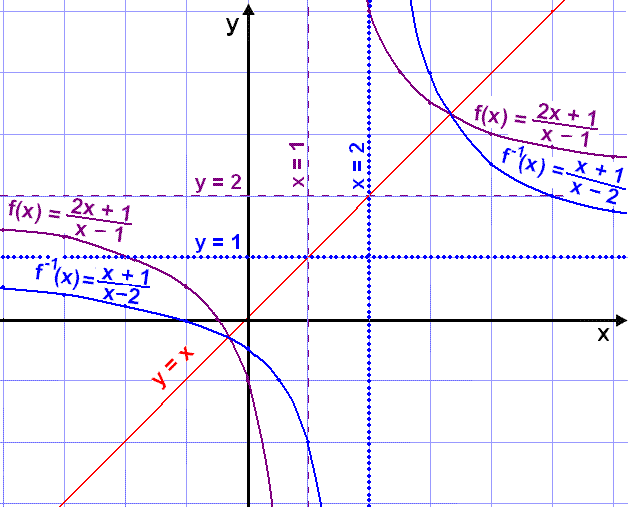
Både grafene og asymptotene speiler hverandre om linjen y = x.

Se på eksemplene, og regn deg gjennom test 6 i Funksjoner 2.
Husk å fylle ut sjekklisten underveis.