© 2008 Rasmus ehf og Jóhann Ísak
© 2008 Rasmus ehf og Jóhann Ísak |
Funksjoner I |
|
La oss se på 2.grads polynomer igjen. Den enkleste formen til funksjonen er f(x) = x2. Grafen er en parabel som kan kalles basisparabelen.
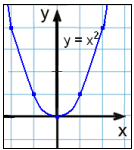
Legg merke til at grafen er symmetrisk om y-aksen. Y-aksen er symmetriaksen til denne funksjonen.
Nå skal vi se på hvordan koeffisientene påvirker utseendet til grafen.
Koeffisienten til x2 kalles vanligvis a. Hvis vi ser på parabler med forskjellige verdier, ser vi at noen er videre, og noen er smalere enn basisparabelen, hvor a =
Her er grafene til parabler hvor a = 4, 2, ½ og ¼.
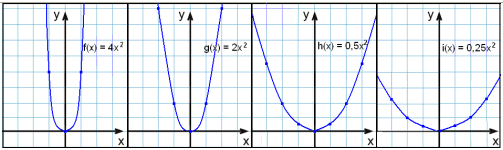
a = 4 a = 2 a = ½ a = ¼
Her er noen parabler med negative verdier av a.
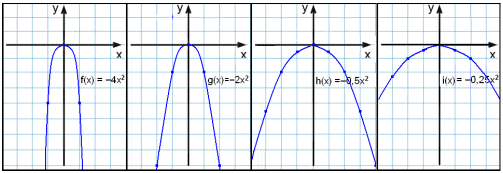
a = −4 a = −2 a = −½ a = −¼
Hvis a er positiv, vender grafen oppover (som en smilemunn!) Jo større verdi, jo smalere graf.
Etter hvert som a blir mindre, blir grafen flatere og flatere, helt til den snur ned (som en sur munn!)
Nå skal vi tegne grafen til f(x) = x2 + 1 og sammenlikne den med g(x) = x2.
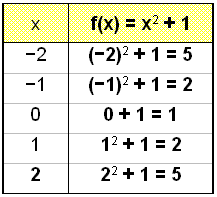 |
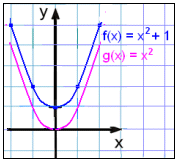 |
Funksjonsverdiene (y-verdiene) i verditabellen for f(x) = x2 +1 er en høyere enn de korresponderende verdiene i verditabellen for g(x) = x2 og grafen har blitt flyttet ned 1 enhet.
Legg merke til at grafen til f(x) = x2 + 1 ikke krysser x-aksen. Dette forteller oss at likningen x2 + 1 = 0 ikke har noen mulige løsninger. Vi vet dette allerede fordi en kvadratrot aldri kan være negativ, så x2 kan aldri være lik -1.
Tegn grafen til f(x) = x2 − 1 og sammenlikn den med g(x) = x2.
 |
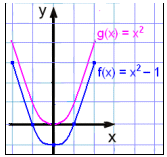 |
Nå er funksjonsverdiene i f(x)-tabellen alle en lavere enn de korresponderende verdiene i tabellen for g(x)= x2 og grafen er flyttet ned en enhet.
Legg merke til at i dette eksemplet krysser grafen f(x) = x2 − 1 x-aksen på to steder.
Dette betyr at likningen x2 − 1 = 0 har to løsninger.
x2 − 1 = 0
x2 = 1
x = ±1
Disse løsningene er x = −1 og x = 1.
Tegn grafen til f(x) = (x + 1)2 (eller f(x) = x2 + 2x + 1) og sammenlikn den med basisparabelen g(x) = x2.
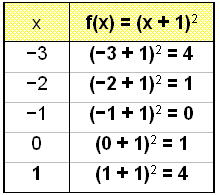 |
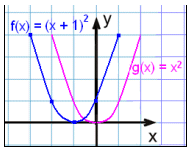 |
Her har vi lagt til 1 til x, og vi kan se at funksjonsverdiene i verditabellen har flyttet seg opp med 1 sammenliknet med basisfunksjonen.
Grafen til f(x) er den samme som hvis vi flytter grafen til g(x) = x2 en enhet til venstre.
Vi sier at grafen har blitt flyttet -1 enhet horisontalt. Symmetriaksen er nå x = −1.
Tegn grafen til f(x) = (x − 2)2 − 1 (eller f(x) = x2 − 4x + 3) og sammenlikn den med grafen g(x) = x2.
Hvis vi bruker samme metode som i forrige eksempel, kan vi gjette at grafen har flyttet seg to enheter til høyre, og en enhet ned. Nå skal vi kontrollere dette ved å lage en verditabell som begynner ved x = 0, og tegne grafen.
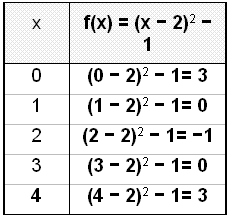 |
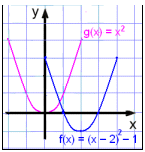 |
Legg merke til at symmetriaksen nå er x = 2.
Vi kan finne ut hvor grafen krysser y-aksen uten å tegne grafen. Dette gjør vi ved å regne ut f(0) = 3 eller ved å gange ut parentesene og undersøke om konstantleddet (leddet uten x) er 3.
f(x) = (x − 2)2 − 1 = x2 − 4x + 4 − 1 = x2 − 4x + 3
eller f(0) = (x − 2)2 − 1 = 4 − 1 = 3
Finn ut hvor grafen f(x) = (x − 2)2 − 1 krysser x-aksen. Vi setter y = f(x) = 0 og løser likningen for å finne x.
(x − 2)2 − 1 = 0 |
Først flytter vi -1 over likhetstegnet. |
(x − 2)2 = 1 |
Så regner vi ut kvadratroten av begge sider av likningen. Husk + og -. |
x − 2 = ±Ö1 = ±1 |
Til slutter vi 2 til den andre siden, og forkorter. |
x = 2 ± 1 |
Skjæringspunktene er x = 2 −1 = 1 og í x = 2 + 1 = 3.
Det er lett å se at å skrive funksjonen som f(x) = (x − 2)2 − 1 gir oss mye informasjon.
Den forteller oss hvor basisgrafen blir flyttet vertikalt og horisontalt.
Den forteller oss også hvor symmetriaksen er.
Dessuten kan vi lett finne skjæringspunktene med x- og y-aksen.
Likningen skrevet på generell form er:
f(x) = a(x + r)2 + s
a er koeffisienten til x2, som vi allerede har sett.
Symmetriaksen har likningen x = −r (eller vi kan si at den har samme verdi som r, men med motsatt fortegn).
Derfor er det viktig å vite hvordan man skriver om funksjonen.
f(x) = ax2 + bx + c på formen f(x) = a(x + r)2 + s
Nå skal vi se på hvordan vi kan gjøre om en annengradslikning fra en form til en annen. Omskriv f(x) = x2 − 4x + 3 på formen f(x) = (x − 2)2 − 1.
Sammenliknet med den generelle formen:
f(x) = ax2 + bx + c
f(x) = x2 − 4x + 3
Her a = 1
og b = −4
og c = 3 (så grafen krysser y-aksen i 3).
Se på regelen for kvadratroten av parenteser: (x ± q)2 = x2 ± 2qx + q2.
Vi ser at koeffisienten til x er 2q.
I vårt eksempel er koeffisienten til x -4, altså er 2q = - 4, og q = -2.
Hvis vi regner ut (x − 2)2, får vi x2 − 4x + 4.
(x − 2)2 = x2 − 4x + 4.
Hvis vi trekker fra 1 på begge sider, får vi:
(x − 2)2 −1 = x2 − 4x + 4−1 = x2 − 4x + 3
Oppsummering av metoden:
f(x) = x2 − 4x + 3 |
Halvparten av koeffisienten til x er −4/2 = −2, som vi opphøyer i andre, og legger til likningen. |
= (x2 − 4x + 22) − 22 + 3 |
|
= (x − 2)2 − 4 + 3 |
Hvis vi legger 4 til likningen, må vi også trekke fra 4. Så forenkler vi −4+3 = −1 |
= (x − 2)2 − 1 |
Fra eksemplet ovenfor kan vi konkludere med at grafen til et 2.grads polynom hvor a = 1 (f(x) = x2 + bx + c) har symmetriaksen i:
x = −b/2 og skjærer y–aksen der hvor y = c.
Finn symmetriaksen til grafen f(x) = 2x2 − 12x + 10.
I dette tilfellet er a = 2, så regelen i forrige eksempel gjelder ikke. Det er heller ikke så lett å skrive om funksjonen som før.
Isteden flytter vi funksjonen ned 10 enheter, ved å trekke 10 fra likningen. Å flytte grafen vertikalt påvirker ikke posisjonen til symmetriaksen.
Vi kaller den nye funksjonen g(x), og finner ut hvor g(x) skjærer x-aksen.
2x2 − 12x = 0
2x(x − 6) = 0
Likningen har løsningene x = 0 og 5, så grafen g(x) skjærer x-aksen i 0 og 6. Symmetriaksen må være midt mellom disse punktene, altså i x = 3.
Skriv om funksjonen f(x)
= 2x2 − 12x + 10 på formen
f(x) = a(x + r)2 + s.
f(x) = 2x2 − 12x + 10 |
Flytt 2 utenfor en parentes. Halvparten av koeffisienten til x er −6/2 = −3, så legg til 32 innenfor parentesen. Vi har egentlig lagt til 18, så nå må vi trekke fra 2×32 = 18 utenfor parentesen. |
= 2(x2 − 6x + 32) − 2∙32+ 10 |
|
= 2(x2 − 6x + 9) − 18 + 10 |
|
= 2(x − 3)2 − 8 |
Nå ser vi at symmetriaksen fortsatt er i x = 3.
Koeffisientene til x i eksempelet ovenfor (f(x) = 2x2 − 12x + 10) er a = 2, b = −12 og c = 10. For å finne symmetriaksen flyttet vi faktoren 2 utenfor en parentes. Dette blir det samme som å dele på 2. Så delte vi koeffisienten til x (−6) på 2.
Den generelle formelen for symmetriaksen til funksjonen
f(x) = ax2 + bx + c er derfor:
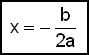
Finn vendepunktet til parabelen f(x) = 2x2 − 12x + 10.
Vendepunktet ligger på symmetriaksen, derfor vet vi x-verdien til vendepunktet (3).
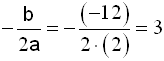
Vi kan finne y-verdien ved å regne ut f(3).
f(3) = 2×32 − 12×3 + 10 = 18 − 36 + 10 = −8.
Vendepunktet til parabelen er (3, −8).
Husk: Hvis a>0 er vendepunktet et bunnpunkt. Hvis a<0 er det et toppunkt.
Prøv
test 3 i Funksjoner 1.
Husk å fylle inn resultatet i sjekklisten din.