© 2007 Rasmus ehf og Jóhann Ísak Pétursson
Funksjoner I
© 2007 Rasmus ehf og Jóhann Ísak Pétursson |
Funksjoner I |
|
Her er noen eksempler på polynomer:
Grad |
f(x) |
Graf: |
0 |
f(x) = a Koeffisient: a |
|
1 |
f(x) = ax+b Koeffisienter: a og b |
|
2 |
f(x) = ax2+bx+c Koeffisienter: a, b og c |
|
3 |
f(x) = ax3+bx2+cx+d Koeffisienter: a, b, c og d |
|
4 |
f(x) = ax4+bx3+cx2+dx+e Koeffisienter: a, b, c, d og e |
|
O.s.v |
||
Koeffisientene a, b, c, osv. er kjente konstanter
som bestemmer formen til polynomet. X er en variabel som kan ha forskjellige
verdier.
Den høyeste potensen av x som er mulig for et
polynom, polynomets grad.
Vi skriver uttrykket med den høyeste potensen av x
først, så de andre i rekkefølge.
Hvis en potens av x mangler, er det fordi koeffisienten er null.
Hvis det mangler koeffisient foran et av leddene, er det fordi koeffisienten er 1.
Finn graden og koeffisientene til polynomet
f(x) = x5 − 2x3 + 4x − 5
Den høyeste potensen til x er 5, så dette er et polynom av 5. grad.
x4 og x2 mangler, så deres
koeffisienter er 0. x5 har ingen synlig koeffisient, så
koeffisienten er 1.
Vi kan tenke oss at leddet uten x er x0, fordi alle tall blir 1 i nulte potens. Nå kan vi skrive ned polynomet på nytt og notere koeffisientene.
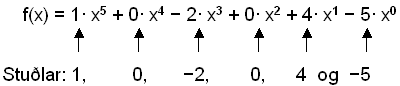Koeffisienter:
Legg merke til at et polynom i 5. grad har 6 koeffisienter. Antallet koeffisienter er alltid en mer enn graden til polynomet.
Potenser i et polynom er alltid hele, positive tall eller null. (I mengden N0). De følgende funksjonene er ikke polynomer.
f(x) = x2 + x + 1 + x−1 + x−2 |
(negativ potens av x) |
g(x) = x2 + x + 1 + Öx |
(x under et rottegn) |
h(x) = x2 + x + 1 + 2x |
(x som potens) |
|
(x i nevner) |
Hvis du ser på polynomenes grafer ovenfor, ser du at et polynom av 0.
grad er en horisontal linje.
Grafen til et 1. grads polynom er en rett, skrå linje.
Grafen til et 2. grads polynom er en parabel. Den har ett vendepunkt.
Grafen til et 3. grads polynom er nesten som 2 parabler satt sammen, den
ene med åpningen ned, og den andre med åpningen opp. Den kan ha to
vendepunkter.
Grafen til et 4. grads polynom er som tre parabler satt sammen, med maks
tre vendepunkter, og slik fortsetter det.
Når graden til polynomet øker, øker også antallet mulige vendepunkt.
Det maksimale antall vendepunkt er alltid en mindre enn graden til polynomet.
På samme måte krysser et 1. grads polynom x-aksen bare en gang, et 2. grads polynom krysser aksen maks to ganger, et 3. grads polynom maks tre ganger osv.
(se på grafene igjen).
Konstantleddet (leddet uten x) forteller oss hvor grafen krysser y-aksen. Dette skyldes at x= 0 på y-aksen, og hvis vi setter x= 0 inn i likningen, sitter vi igjen med bare konstantleddet.
Når f(x) = 2x3 + 3x2 + 4x + 6
f(0) = 2∙03 + 3∙02 + 4∙0 + 6 = 6
Punktet (0, 6) er der hvor grafen krysser y-aksen.
Alle punktene på x-aksen har y-verdien null, så vi kan finne ut hvor grafen krysser x-aksen ved å sette y = 0 og løse likningen for x.
y = f(x) = 0.
Finn punktene hvor polynomet f(x) = 2x + 4 krysser x-aksen og y-aksen.
Skjæringspunktet med y: 4. |
Konstanten i formelen for f(x) er 4. |
Skjæringspunktet med x: 2x + 4 = 0 |
Sett f(x) = 0. |
x = −4/2 = −2 |
Løs likningen for å finne x. |
Skjæringspunktet med x er altså −2. |
Finn skjæringspunktene til polynomet f(x) = x2 − 2x med x- og y-aksen.
Skjæringspunktet med y er 0. |
Konstanten i formelen for f(x) er 4. |
Skjæringspunktet med x: 2x + 4 = 0 |
Sett f(x) = 0. |
x (x − 2) = 0 |
Faktoriser og løs likningen for å finne x. |
Polynomet krysser x-aksen i to punkter, x= 0 og 2. |
Finn skjæringspunktene til polynomet f(x) = (x − 1)(x − 2)(x − 3) med x- og y-aksen.
Hvis vi undersøker
likningen, ser vi at når man multipliserer parentesene sammen, blir
konstantleddet -6.
Hvis du ikke ser det, kan du finne konstanten ved å gange ut parentesene.
(x − 1)(x − 2)(x − 3) = (x2 − 2x − x + 2)(x − 3)
= (x2 −3x + 2)(x − 3)
= x3 − 3x2 − 3x2 + 9x + 2x − 6
= x3 − 6x2 + 11x − 6
En enklere måte å finne skjæringspunktet, er å regne ut f(0) uten å gange sammen parentesene.
f(0) = (0 − 1)(0 − 2)(0 − 3) = −6
Skjæringspunktet med y er ved = −6.
For å finne ut hvor grafen krysser x-aksen må vi løse likningen
(x − 1)(x − 2)(x − 3) = 0
Den eneste måten dette kan bli null, er hvis en av faktorene (her parentesene) blir 0. Dette er når x = 1, 2 eller 3. Derfor krysser grafen x-aksen når x=1, x=2 og x=3.
Ligger punktene (1, 6) og (2, 8) på grafen til funksjonen f(x) = x2 + 4x + 1.
f(1) = 12 + 4∙1 + 1 |
Regn ut f(1). |
= 1 + 4 + 1 = 6 |
Punktet (1,6) er altså på grafen.
f(2) = 22 + 4∙2 + 1
= 4 + 8 + 1 = 13
Punktet (2,8) er altså ikke på grafen.
Finn likningen til et 1. grads polynom (en rett linje) som går gjennom punktene (1, 1) og (2, 3).
Vi kaller funksjonen f(x) = ax + b
f(1) = a∙1 + b = 1 får vi likningen a + b = 1 |
Når vi setter inn verdiene (1, 1) |
f(2) = a∙2 + b = 3 får vi likningen 2a + b = 3 |
Når vi setter inn verdiene (2, 3) |
f(2) − f(1) = (2a + b) − (a + b) = 3
− 1 |
Løs
likningene |
Likningen til polynomet (linjen) er f(x) = 2x − 1.
Finn et 2.grads polynom (en parabel) hvor grafen går gjennom punktene (0, 6), (1, 0) og (3, 0).
Kall funksjonen f(x) = ax2 + bx + c og regn ut a, b og c.
(0, 6) er skjæringspunktet med y, så c = 6.
(1) = a∙12 + b∙1 + 6
= a + b + 6 = 0
f(3) = a∙32 + b∙3 + 6 = 0 |
 |
Gjør likningen enklere ved å dele alle leddene på 3. |
f(3) = f(1) = 0
3a + b + 2 = a + b + 6
3a − a + b − b = 6 − 2
2a = 4
a = 2
f(1) = 2 + b + 6 = 0
b = −2 − 6 = −8
Derfor er polynomet f(x) = 2x2 − 8x + 6
Prøv
test 2 i Funksjoner 1.
Husk å fylle inn resultatet i sjekklisten din.
