Faktorisering.
| © 2007 Rasmus ehf og Jóhann Ísak Pétursson |
Faktorisering. |
|
Introduksjon 5 Parenteser som er felles faktorer
| Du vet hvordan du multipliserer de to parentesene.. | ||
|
(a + b)(c + d) = ac + ad +
bc
+ bd
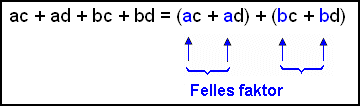
Dersom du har uttrykket på høyre side, hvordan kan du gjøre det om til de to parentesene på venstre side? Her er en systematisk måte å gjøre det på. Sett først leddene sammen i parenteser to og to, og merk deg at hver parentes har en felles faktor. |
||
 |
||
| Sett disse faktorene utenfor parentesene. | ||
|
|
=
(c + d)(a + b)
Felles faktor settes utenfor parentesen |
|
|
altså en felles faktor |
||
|
Med andre ord er parentesene felles faktorer i uttrykket og kan bli faktorisert ut . |
||
|
|
||
|
Dersom du synes dette er vanskelig å forstå, tenk på parentesene som en enkelt verdi, vi kan kalle den S. Nå ser uttrykket slik ut: ac + ad + bc + bd = (ac + ad) + (bc + bd) |
||
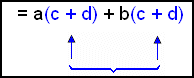 |
||
| Kall parentesen S | ||
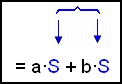 |
og skriv S i stedet for parentesen (c + d). | |
| = S(a + b)= (c + d)(a + b) |
Sett S utenfor parentesen. |
|
|
Til slutt settes parentesen (c + d) tilbake i stedet for S. Legg merke til at det ikke har noe å si hvilket par vi setter sammen. Hvis vi stokker om på leddene og setter de i parentes vil eksemplet se slik ut: |
||
| ac + ad + bc + bd | = (ac + bc) + (ad + bd) | |
|
= c(a + b)+ d(a + b) = (c(a + b) + d(a + b)) = (a + b)(c + d) Sluttresultatet er det samme. |
||
Eksempel 1
| Faktoriser x2 + x + ax + a. | |
|
x2 + x + ax + a |
= x(x + 1) + a(x + 1) |
| = (x + 1)(x + a) | |
Eksempel 2
|
Faktoriser x3 − 4x2 − x + 4. |
|
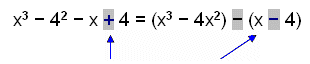 |
|
|
Legg merke til at pluss tegnet forandres til minus når vi setter det i en parentes med minus foran. Dette gjør at uttrykket blir det samme hvis vi fjerner parentesene igjen. |
|
|
= x2(x − 4) − (x − 4) |
= (x − 4)(x2 − 1) |
|
|
= (x − 4)(x + 1)(x − 1) |
Eksempel 3
|
Faktoriser 6x2 + 13x + 6. |
|
| 6x2 + 13x + 6 = 6x2 + 4x + 9x + 6 | |
|
Først må vi dele opp 13x i to deler. For å finne disse multipliserer vi koeffisienten til x2 , 6, med den konstante koeffisienten, altså 6. Dette gir 36. Nå må vi finne de to tallene som vi adderer og får 13, men der produktet blir 36 når vi multipliserer dem. Disse tallene finner vi enkelt, de er 4 og 9. Så vi deler 13x opp i 4x og 9x. Nå kan vi faktorisere ut en parentes |
|
| = (6x2 + 4x) + (9x + 6) | = (2x(3x + 2) + 3(3x + 2)) |
| = (3x + 2)(2x + 3) | |
Prøv test 5 om faktorisering. Scorer du 80%, eller mer, kan du gå til neste emne.