© 2007  Rasmus ehf  og Jóhann Ísak Pétursson

Faktoriseringsuttrykk

 Print

Øvelse 4    Faktorisering ved prøving  

La oss gjenta hvordan vi multipliserer parenteser.
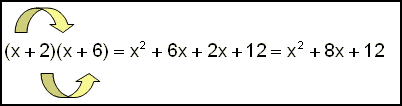Hvert ledd i en parentes blir multiplisert med hvert ledd i den andre parentesen.

Dersom vi bruker bokstaver isteden for tall, ser uttrykket slik ut:

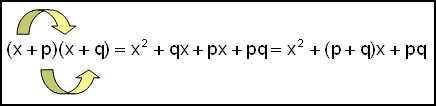Faktorisering betyr å gå i motsatt retning, å sette leddene tilbake i de to parentesene.

Vi må finne to hele tall p og q slik at når vi multipliserer dem med hverandre får vi 12 og når vi legger dem sammen får vi 8.

La oss prøve noen tall. Vi kan kalle det minste tallet p og det største tallet q.

Her er to hele tall vi må bruke.

p∙q

p+q

1∙12 = 12

1+12 = 13

 2∙6 = 12

 2+6 = 8

 3∙4 = 12

  3+4 = 7
Vi ser lett at  p = 2 og q = 6 tilfredsstiller våre krav.   

Svaret er:       

Exempel  1

Faktoriser x2 − 7x + 12

I dette eksemplet må både p og q være negative tall. Vi vet dette fordi de må være positive når de multipliseres med hverandre men negative når de legges sammen. Når to negative tall blir multiplisert med hverandre blir svaret et positivt tall.
Dersom leddet uten x er positivt og leddet med x er negativt, må både p og q være negative.

 

 Tallene vi må sjekke står i denne tabellen:

 

p∙q

p+q

 (−1)∙(−12) = 12

−1−12 = −13

   (−2)∙(−6) = 12

  −2−6 = −8

   (−3)∙(−4) = 12

  −3−4 = −7
Verdiene p = −3 og q = −4 passer i vårt eksempel.
Løsningen er derfor:

Eksempel 2

Faktoriser  x2 + 4x − 12

I dette eksemplet må p og q ha motsatte fortegn fordi vi får et negativt tall når vi multipliserer dem med hverandre. Når vi legger tallene sammen blir svaret derimot positivt og dette betyr at det største tallet (  q )  må være positivt.
Hvis to tall som multipliseres med hverandre får et negativt svar, må det ene tallet være positivt og det andre negativt.

 

 Tallene vi må sjekke ser du i denne tabellen:

 

p∙q

p+q

 (−1)∙(12) = −12

−1+12 = 11

  (−2)∙(6) = −12

  −2+6 = 4

  (−3)∙(4) = −12

  −3+4 = 1
Tallene p = −2 og q = +6 tilfredsstiller våre krav.
Løsningen er derfor:

Eksempel 3

Faktoriser x2 − x − 12

I dette eksemplet må tallene p og q ha motsatt fortegn. Summen deres er nå negativ så dette betyr at det største tallet (  q )  må være negativt.
Dersom produktet er negativt må en faktor være positiv og den andre negativ( +  - )

 

 Tallene vi må sjekke ser du i denne tabellen:

 

p∙q

p+q

 1∙(−12) = −12

1−12 = −11

   2∙(−6) = −12

  2−6 = −4

3∙(−4) = −12

 3−4 = −1
De korrekte tallene er p = 3 og q = −4
Løsningen er derfor

Prøv nå test 4 i faktorisering. Dersom du får 80% eller mer korrekt, kan du fortsette på øvelse 5.