Geometri
| © 2006 Rasmus ehf |
Geometri |
Introduksjon 5.
Arealer:
Enheter for areal:
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 1 | 00 | 00 |
| 1m2 = 100dm2 = 10000cm2 |
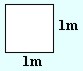 |
A = 1m · 1m = 1m2 |
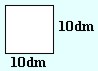 |
A = 10dm · 10dm = 100dm2 |
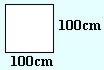 |
A = 100cm · 100cm = 10000cm2 |
Du kan beregne arealet av forskjellige geometriske figurer, f.eks.:
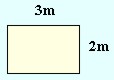 |
||
| A = | 3m · 2m = 6m2 | |
A = seks kvadratmeter.
Hvis du skal gi svaret i kvadratcentimeter, kan du bruke tabellen for arealenheter:
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 6 | 00 | 00 |
| 6m2 = 60000cm2 |
En annen bra måte å løse oppgaven på er ved å forandre meterenheten til centimeter før utregningen:
 |
= |
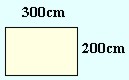 |
| A = 300cm · 200cm = 60000cm2 | ||
Samlet overflate av en kasse. Du må beregne arealet av alle seks sidene.
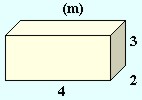 |
3m · 4m = 12m2 | |
| 2m · 3m = 6m2 | ||
| 2m · 4m = 8m2 |
12m2 + 6m2 + 8m2 = 26m2
Dette var kun tre av sidene. Kassen har tre andre sider som er akkurat like store.
Det totale arealet blir derfor: 26m2 · 2 = 52m2
For at kunne beregne overflaten av en romfigur må en vite arealet av dens sideflater.
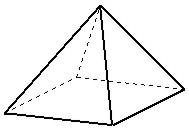
|
Samlet overflate av en pyramide = kvadratets areal + fire trekanters arealer. |
||||||||
 |
+ |  |
+ |  |
+ |  |
+ |  |
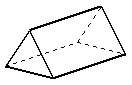
| Arealet av et prisme = |  |
+ |  |
+ |  |
+ |  |
+ |  |
Den krumme veggen
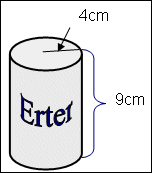
| Overflaten av en sylinder (Her illustrert med en hermetikkboks)= | ||||
|
|
+ |
|
+ |
|
| Toppen + bunnen + den krumme etiketten rundt boksen | ||||
| Lokkets areal | A = r2 · π = 4·4 · π = 50,24cm2 |
| Bunnens areal | Samme areal som lokket |
Den krumme veggen brettes ut så det får form som et rektangel ( etiketten rulles ut )
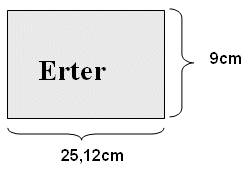 |
A = lengde
· bredde =
9cm · 25,12cm = 226,08cm2 |
| Denne siden svarer til sirkelens omkrets.
|
| Sylinderens (hemetikkboksens) overflate. | ||||
|
|
+ |
|
+ |
|
| A = 50,24cm2 + 50,24cm2 + 226,08cm2 = 326,56cm2 | ||||
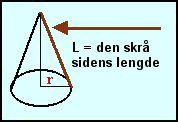 |
Arealet af en kjegles krumme overflate = |
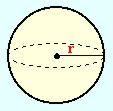 |
Arealet av en kule = |
Sett deg grundig inn i dette kapittel og gjør deretter test 5 i geometri: