Prósentureikningur.

© des.1999 Hugo og Tómas Rasmus        

    Kynning 5

Ef þú hefur gott vald á prósentuköflunum hér á undan hefur þú allar forsendur til að reikna allan almennan prósentureikning í daglegu lífi og það sem fengist er við í grunnskólanum.

    Þyngri verkefni í prósentureikningi koma nú hér á eftir og er nauðsynlegt að rýna í og skilja textann til að finna atriði sem skipta máli.  Svo má nota þær reikniaðferðir sem hafa verið kynntar.

Dæmi:  

Þegar eitthvað hækkar eða lækkar.

Verð á jakka sem kostar 6000 kr. lækkar um 25%.  Hvert verður nýja verðið?

Finnum út að lækkunin er:   

Eða við sjáum að 

og finnum beint nýtt verð:

Ef jakkinn hefði hækkað um 25 % hefðum við lagt hækkunina við:

Verð á jakka + hækkun = nýtt verð

Eða hugsað:

Dæmi:  

Samanburður.

Launin hjá Sigga og Stjána hækka um næstu mánaðarmót um 5% hjá hvorum um sig.  Fá þeir sömu hækkun?  Þessu er ekki hægt að svara nema vita hvað þeir voru með í mánaðarlaun fyrir hækkun.  Siggi var með 125000 og Stjáni með 145000.

Nú getum við reiknað.

Hækkun hjá Sigga er : 

Hækkun hjá Stjána er: 

Þegar bornar eru saman tölur verða viðmiðunartölurnar að vera klárar.  Viðmiðunartalan er 100%.

Dæmi:  

Ef Siggi úr dæminu á undan segði mér að hann hefði hækkað í launum um 5% og væri með eftir hækkun 131250 þá dyggðu þessar upplýsingar til að reikna út hvað hann var með fyrir hækkun.

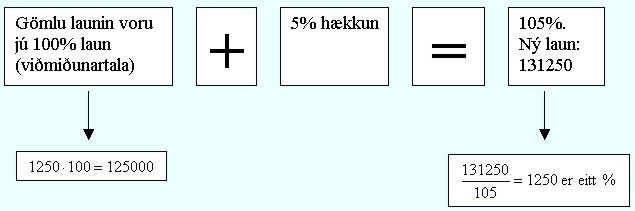
Sama dæmi með prósentujöfnunni:

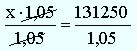
Dæmi:  

hækkun milli ára.

Nýr bíll kostar 1500000 um áramót 1998 og hækkar um 12% á ári.  Hvað kostar hann um áramótin 2000?

Finnum 12% hækkun:    

Nýtt verð:    um áramótin 1999

Finnum aftur 12% hækkun á nýtt viðmiðunarverð

Verð um áramót 2000 er því:

Taktu nú próf 5 í prósentum.