Statistik
| © 2005 Rasmus ehf |
Statistik |
|
Instruktion 5.
Cirkeldiagrammer. Vildledende grafer og diagrammer
Man kan inddele cirkler og måle dem i procent og grader.
|
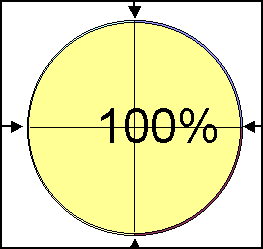
En hel cirkel er 100 % |
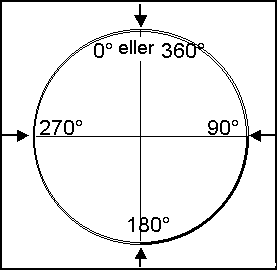
Cirklens periferi dækker 360 grader |
|
 |
|
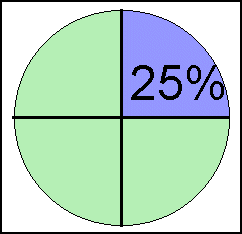
1 % af en cirkel svarer til |
eller
|
 |
 |
Cirkeldiagram
Tegn en cirkel, hvor 35% er farvet rød, 45% grøn og 20% blå.
Husk: 1% = 3,6º
| Farve | Udregnet gradtal | 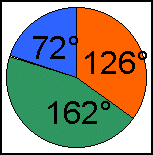 |
| rød | ||
| grøn | ||
| blå |
Det er nødvendigt at øve sig på dette. Du skal bruge en passer og en
vinkelmåler.
Begynd med at markere cirklens centrum med et kryds. Placer passerens nål i
krydset.
Tegn en cirkel med passeren. Marker cirklens radius ved at tegne en ret
linie fra centrum til cirklens periferi.
Nu bruger du vinkelmåleren til at måle den røde vinkel. Afsæt en prik ud for
1260 og tegn radius fra centrum gennem prikken til cirklens periferi.
Farv området mellem disse radier (de 126 grader) rødt.
Brug samme fremgangsmåde til den grønne og den blå vinkel.
Du kan også tegne cirkeldiagrammer hvis du bruger et regneprogram, f.
eks. Excel. Du skriver tallene, og programmet foretager udregninger, tegner
cirklen og inddeler den. Det er udmærket at kunne bruge begge metoder.
| Farve | Udregnet gradtal |  |
| rød | ||
| grøn | ||
| blå |
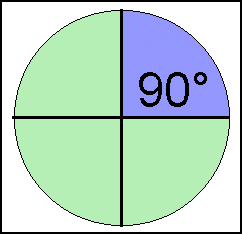
Sådan kan du beregne procenttallet, når du kender gradtallet. For eksempel 72 grader:
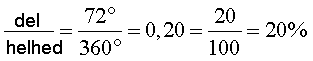
Vildledende grafer
og diagrammer
Grafer og diagrammer kan ofte være vildledende.
|
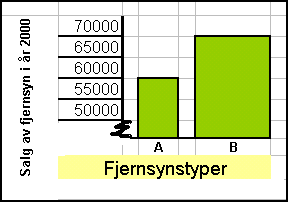
Eksempel 1: Salg af fjernsyn
|
|
|
·
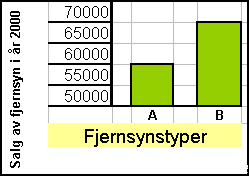
Der er solgt 70000 fjernsyn af type A ·
Der er solgt 60000 fjernsyn af type B
|
| Lad os sige at en person ønsker at fremhæve type B frem for type A.
Ved at vise en graf som denne ser det ud som om type B er dobbelt så
populær som type A. Det nederste af grafen (de første 50000 apparater
) er skåret væk og inddelingen på 2. aksen er blevet mere detaljeret. |
 |
|
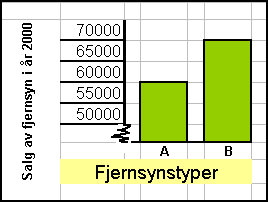
Hvis en akse ikke begynder ved nulpunktet, skal aksen vises som en brudt
linie ( zigzag-linie) som fastslår, at ikke hele aksen er medtaget. Her er den lodrette akse (2. aksen) tegnet som en brudt linie, for at
vise at aksen ikke begynder i 0. |
 |
Der kan dog bruges andre små fiduser for at snyde med
diagrammer/grafer.
Fejlagtig information anvendt i grafiske afbildninger..
Upræcise størrelsesforhold benyttet i grafiske afbildninger.
Eksempel 2: Salg af fjernsyn
| Den lidt utroværdige person fra før blev naturligvis belært om at det er snyd ikke at lave en brudt akse, så han måtte rette dette i sin næste graf. | Grafernes størrelse er dog stadig vildledende. |
|
Det ser nu ud til at salget af type B er næsten fire gange så stort
som type A, da arealet af type B´s graf er næsten fire gange så stort
som type A´s. Hvad er galt med denne graf? Søjlen for type B er tegnet dobbelt så bred som søjlen for type A. |
|
Dette er naturligvis også vildledende for opfattelsen af oplysningerne.
·
Statistiske størrelser illustreret i et diagram skal altid være præcise.
·
Er det ikke tilfældet er diagrammet misvisende.
Det er vigtigt at kunne tolke de korrekte oplysninger fra den store mængde af information vi hele tiden modtager fra TV og aviser.
Men statistik kan bruges efter forgodtbefindende.
For eksempel er det farligste sted at opholde sig statistisk set hjemme
i sin seng…….Langt mere end 90 % af alle mennesker dør i deres seng!!!!!
Når det farligste sted at være i trafikken er i et vejkryds, kunne man
forledes til at tro at det gjaldt om at speede farten op når man nærmer et
vejkryds… Det gælder jo om at komme ud af det farlige område så hurtigt som
muligt. Denne form for
statistiklogik er jo helt hen i vejret!!
Arbejd lidt med disse ting og gå så til test 5 i Statistik.