Ligninger 1
| © 2005 Rasmus ehf |
Ligninger 1 |
Introduktion 3.

Ligninger med parenteser.
Der findes to slags parenteser. Plusparenteser og minusparenteser.
En plusparentes ( der står ikke et minustegn foran parentesen) kan hæves uden
videre.
En minusparentes ( der står et minustegn foran parentesen) kan kun hæves hvis
alle fortegn inde i parentesen ændres. + ændres til -, og - ændres til +.
Eksempel 1:
| 6x -(2x - 1) =(6x - 3x) + 4 | |
| 6x - 2x + 1 = 6x - 3x + 4 | 1. Hæv parentesen |
| 4x + 1 = 3x +4 | 2. Ensbenævnte udtryk samles på hver side af lighedstegnet. |
| 4x - 3x = 4 - 1 | 3. De kendte - tallene - samles på højre side. |
| x = 3 | 4. Svar: x = 3. |
Eksempel 2:
| 2(3x + 2) - 3(7 + x) = 1 | |
| 6x + 4 - 21 - 3x = 1 | 1. Gang ind i parentesen. |
| 3x - 17 = 1 | 2. Udtrykkene samles og beregnes på begge sider af parentesen. |
| 3x = 1 + 17 | 3. Tallene flyttes over på højre side af lighedstegnet. |
| 3x = 18 | 4. Del med 3 på begge sider af lighedstegnet. |
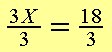 |
|
| x = 6 | 5. Svar: x = 6. |
Eksempel 3:
| 2(x + 2) - 5x = 2x - 11 | |
| 2x + 4 - 5x = 2x - 11 | 1. Gang ind i parentesen. |
| -3x + 4 = 2x - 11 | 2. Udtrykkene samles og beregnes på begge sider af parentesen. |
| 4 + 11 = 2x + 3x | 3. X placeres på højre side. |
| 15 = 5x | 4. Del med 5 på begge sider af lighedstegnet. |
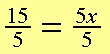 |
|
| 5. Svaret bliver 3 = x, eller pænere: x = 3. |
(Nogle gange er det mest praktisk, at x står på højre side af lighedstegnet, da det kan være nemmere at arbejde med positive størrelser.)
Træn lidt med eksemplerne og gå til test 3 i ligninger.
Husk indimellem at udfylde din checkliste.