© 2005  Rasmus ehf

Brøker (multiplikation og division)

Print

Introduktion 1.

At forkorte og forlænge en brøk.

Vi repeterer kort emnet opdeling i faktorer (fælles divisor). 

Et eksempel: 

Tallet 6 kan udtrykkes med faktorerne 2 og 3.
Altså er tallene 2 og 3 divisorer i tallet 6. 

Alle tal har divisorer, to eller flere - bortset fra primtallene (2,3,5,7,11,13,17,19,23,...o.s.v.)

Ind imellem fås udtryk, som kun består af bogstaver, men disse kan også opdeles i faktorer.

Et eksempel:     

Tallet 1 har ingen betydning ved multiplikation, så derfor skrives det ikke.

Husk at brøkstreg altid betyder division.

Vi ser på nogle eksempler på, hvordan man ved hjælp af fælles divisorer kan forkorte en brøk

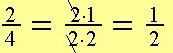
  Vi ser at:

og

Den fælles divisor er 2. Vi forkorter brøken med 2.

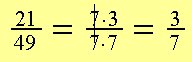
   Vi ser at:

og

Den fælles divisor er 7. Vi forkorter brøken med 7.

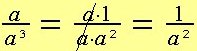
  Vi ser at:

og

Værdien a er fælles divisor. Vi forkorter brøken med a.

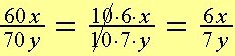
  Vi ser at:

og

Den fælles divisor er 10. Vi forkorter brøken med 10.

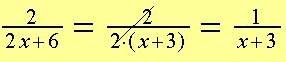
Vi sætter først 2 udenfor parentes (2X + 6) = 2(x + 3)

Fælles divisor er 2. Vi forkorter med 2.

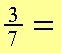
Primtal har kun tallet selv og 1 som divisorer. Brøken består af primtal og har ingen fælles divisorer. Brøken kan derfor ikke forkortes.

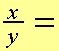
Forskellige variabler har også kun sig selv og 1 som divisorer. Der er altså heller ingen fælles divisorer her, så brøken kan ikke forkortes.

Udfør nu test 1 i Multiplikation og division med brøker.