© 2007  Rasmus ehf  og Jóhann Ísak Pétursson

Faktorisering af toleddede størrelser

Vi repeterer reglerne for multiplikation af en toledet størrelse

Hvert led i den første parentes multipliceres med hvert led i den anden parantes.

Bruger vi bogstaver i stedet for tal, ser udtrykket sådan ud:

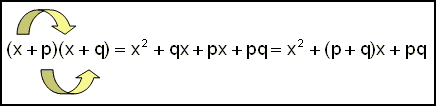Faktorisering betyder at vi går den modsatte vej idet vi sætter leddene tilbage i de to parenteser.

Vi skal finde to hele tal p og q som ved en multiplikation har resultatet 12 og lagt sammen har resultatet 8.

Lad os prøve med vilkårlige tal. Vi kan kalde det mindste tal for p og det største tal for q.

Vi kan se at  p = 2 og q = 6 tilfredsstiller de stillede krav.     

Svaret er:       

I dette eksempel må både p og q være negative tal. Vi ved det, da de må være positive når de multipliceres med hinanden, men negative når de lægges sammen. Når to negative tal multipliceres med hinanden bliver resultatet et positivt tal.

Da leddet uden x er positivt og leddet med x er negativt, må både p og q være negative.

Tallene vi må afprøve står
i denne tabel:

Værdierne p = −3 og q = −4 passer i vores eksempel.   

I dette eksempel må p og q have modsat fortegn, da vi får et negativt tal når vi multiplicerer dem med hinanden. Når vi lægger tallene sammen, skal svaret derimod være positivt, og det betyder, at det største tal (q) må være positivt

Hvis to tal multipliceres med hinanden og resultatet er negativt, må det ene tal være negativt mens det andet tal er positivt.

Tallene vi må afprøve står
i denne tabel:

Tallene p = −2 og q = +6 tilfredsstiller vores krav

Løsningen er derfor:

I dette eksempel må tallene have modsat fortegn. De to tals sum er negativ hvilket betyder, at det største tal (q) må være negativt

Da de to tals produkt er negativt, må den ene faktor være positiv og den anden negativ (+ - )

Tallene vi må afprøve står
i denne tabel:

De korrekte tal er p = 3 og q = −4

Løsningen er derfor