© 2008  Rasmus ehf og Jóhann Ísak Pétursson

Eksponenter og logaritmer

Introduktion 3
Naturlige logaritmer

Nu da computere og lommeregnere kan foretage udregningerne for os, har vi ikke behov 10-logaritmen så ofte længere. Der findes derimod en anden logaritme, som er blevet vigtigere på flere områder.

Denne funktionen kaldes den naturlige logaritme, og har symbolet  
ln.  f(x)=ln x

Den naturlige logaritme er baseret på tallet e, som vi har på lommeregneren.

e er et irrationalt tal. e 2.718

Sådan finder du den naturlige logaritme til 2 på en CASIO-lommeregner:

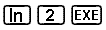
Svaret er ca. 0.693, som viser, hvad vi må ophøje e til for at få 2.

   e^0.693 2

Kontroller dette på lommeregneren:

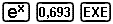
Lommeregneren viser følgende resultat:   1,9997 2.

Funktionerne f(x) = ln x og g(x) = e^x ophæver hinanden, når den ene bruges som resultatet af den anden. Det samme sker med f(x) = log x og g(x) = 10^x eller når man kvadrerer et tal og senere finder kvadratroden. En anden måde at sige dette på, er at funktionen       

f(x) = ln x er det modsatte af funktionen g(x) = e^x.

 ln e^x = x og e^{ln x} = x

Tallet e er irrationalt, og har ingen eksakt værdi.
Vi kan beregne det med et hvilket som helst antal decimaler ved at vælge større og større værdier for x og sætte dem ind i denne formel:

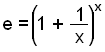
Beregn e ved at indsætte x = 1000 i formlen, og ved at bruge en lommeregner.

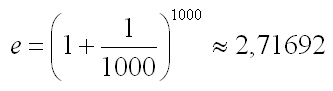
I EXCEL har e værdien 2.7182818284591. Så ved at vælge x = 1000 får vi kun 2 rigtige decimaler.

Prøver vi så med x = 1000000,

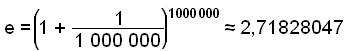
når vi op på 5 rigtige decimaler.

Jo højere x vi vælger, jo mere nøjagtig e kommer vi frem til.

Tegn graferne til funktionen f(x) = ln x og til funktionen g(x) = e^x.

Først laver vi en værditabel (et sildeben):

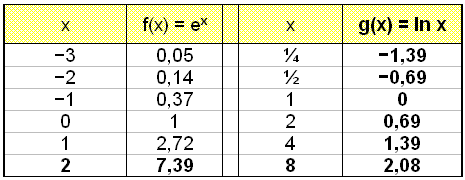
Læg mærke til, at der ikke er nogen negative værdier i kolonnen til f(x) = e^x og der er heller ingen negative værdier i x-kolonnen for den modsatte funktion g(x) = ln x.

Definitionsmængden til f(x) = ln x  er mængden F_f  =  { xÎR | x > 0 }.

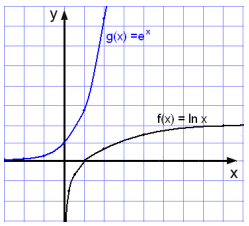
Bemærk at vi tegner begge grafer i samme koordinatsystem, fordi de er spejlbilder af hinanden. De er symmetriske, og symmetriaksen er linjen y = x.

Dette gælder altid for graferne til to modsatte funktioner.

Reglerne for 10-logaritmen (log) gælder også for den naturlige logaritme (ln)

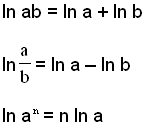
Her er nogle eksempler, som viser, hvordan du kan bruge dette.

a)

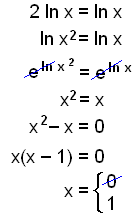Flyt 2-tallet og skriv som potens. Indsæt basetallet e på begge sider af lighedstegnet. e og ln ophæver hinanden, så vi står tilbage med en andengradsligning. Flyt x til den anden side af lighetstegnet. Faktoriser og løs ligningen.

    x = 0 er umulig, da det ikke er mulig at skrive 0 som en potens ( e^x 0 ).

b)

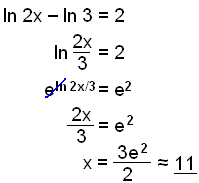Skriv venstre side som en logaritme. Indsæt basetallet e. ln og e ophæver hinanden.Løs ligningen.

c)

Reducer ved at skrive som en logaritme.
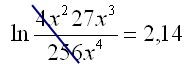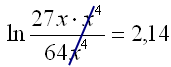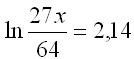Indsæt e på begge sider af lighedstegnet og løs ligningen

Løs ligningerne:

a)

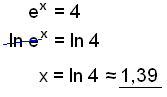Find logaritmen til begge sider..

b)

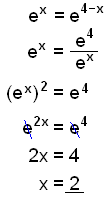Brug reglerne: a xa y = a x+y ,  a x/a y = a x−y og  (a n)m = a nm   til at skrive begge sider som en potens af e.

c)

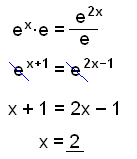Brug reglerne: a xa y = a x+y og  a x/a y = a x−y til at skrive begge sidene som en potens af e

Løs ligningerne:

a)

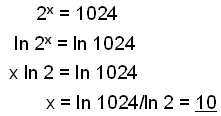Find log til begge sider af lighedstegnet og bruk reglen a x= x ln a, for at flytte den ukendte værdien ned foran ln.

b)

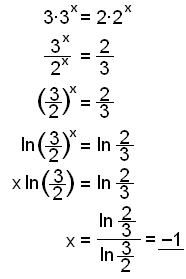Flyt leddene i ln x til den ene side af lighedstegnet og de andre til den anden side. Reducer ved hjælp af potensreglerne. Find log til begge sider for at flytte x ned og find så x.

c)

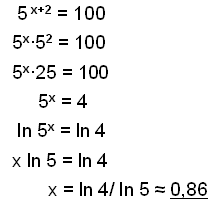Skil eksponenterne til roden 5 fra hinanden. Divider på begge sider med 25, og find x som ovenfor beskrevet.

Prøv test 3 i Eksponenter og Logaritmer.  

Husk at bruge checklisten.