© 2008 Rasmus ehf og Jóhann Ísak Pétursson
© 2008 Rasmus ehf og Jóhann Ísak Pétursson |
Eksponenter og logaritmer |
|
Introduktion 2
Logaritmer baseret på 10.
Der er få tal, som er lige så lette at arbejde med, som 1, 10, 100, 1000 osv. Skal man gange dem sammen, tæller man blot antal nuller.
F.eks. 10∙100∙1000 = 1 000 000, totalt 6 nuller.
Det samme ser vi, når vi skriver tallene som potenser af 10.
10∙100∙1000 = 101∙102∙103 = 101+2+3 = 106 = 1000000.
Det vil sige, at ved potenser, hvor roden er 10, angiver eksponenten, hvor mange nuller der skal skrives.
For rundt 400 år siden fandt matematikerne ud af, at skrive tal som potenser af 10, ville gøre multiplikationen meget lettere. I stedet for at gange tallene med hinanden, kunne man nøjes med at lægge eksponentene sammen. I en tid, hvor der ikke fandtes lommeregnere, var man glad for alt, som kunne gøre en udregningen lettere.
En funktion kaldt logaritme blev defineret, og skrives som: f(x) = lg x eller f(x) = log x hvor log x er potensen, som 10 opløftes til for at blive x.
Funktionen f(x) = log x er defineret for alle positive tal, og den finder den potens som 10 skal opløftes til for at give x.
Vi kan kun finde logaritmen til positive tal, da potenser af 10 altid er positive.
Definitionsmængden til funktionen f(x) = log x er derfor:
{ xÎR
| x > 0 }.
Nu skal vi se, hvordan vi arbejder med logaritmer på en lommeregner. Der findes mange lommeregnere med funktionensknappen log, men her bruger vi en ”Casio grafisk” lommeregner.
Sådan finder du log 2:

![]()
f(1) = lg 1 = 0 fordi 100 = 1
f(2) = lg 2 ≈ 0,303 fordi 100,303
2
f(3) = lg 3 ≈ 0,477 fordi 100,477
3
f(10) = lg 10 = 1 fordi 101 = 10
f(20) = lg 20 ≈ 1,303 fordi 101,303
20
f(100) = lg 100 = 2 fordi 102 = 100
f(1000) = lg 1000 = 3 fordi 103 = 1000
Funktionen
f(x) = log x er den modsatte af funktionen g(x) = 10x. Dette betyder,
at vi nu også kan gå den modsatte vej, på samme måde som når vi kvadrerer (a x
a=a²), og derefter finder kvadratroden til resultatet(![]() a²
= a)
a²
= a)
| Løs ligningen 10x = 2 | Vi finder log til begge sider af ligningen. Da funktionerne log x og 10x ophæver hinanden, får vi blot x på venstre side. Kontroller resultatet på lommeregneren. |
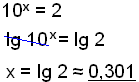 |
| Løs ligningen lg x = 4 | Vi ændrer begge sider af ligningen så de bliver til potenser af 10. Funktionerne log x og 10x ophæver hinanden, så x blir stående alene tilbage på venstre side. |
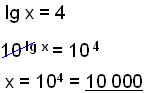 |
Logaritmer er bare eksponenter. Derfor gælder følgende regler for logaritmer.
Vi ved, at 10x×10y = 10x+y. Derfor ved vi også, at
x = log a og y = log b.
og deraf følger at log ab = log a + log b.
På samme måde ser vi, at log a/b = log a − log b.
Vi kan skrive:
log an = log a + log a + ∙ ∙ ∙ ∙ + log a(n værdier) = n log a.
Deraf kan man udlede de følgende logaritmeregler:
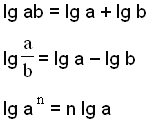
Logaritmereglene bliver brugt, når man som i følgende reducerer udregningen til én logaritmisk betegnelse:
a) lg a + lg b + lg c = lg abc
b) lg a + lg 2b + lg 3c + lg 4 = lg a∙2b∙3c∙4 = lg 24abc
c) lg a + lg a + lg a = 3 lg a = lg a3
d) lg 2a − lg 2b = lg 2 + lg a − lg 2 − lg b = lg a/b
e) ¼∙(lg a + lg a3) = ¼∙(lg a + 3 lg a) = ¼∙4 lg a = lg a
Løs ligningen ved at skrive venstre side af ligningen som en logaritme.
a)
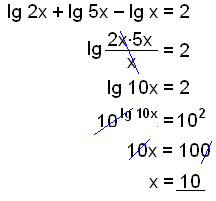 |
Vi starter med at bruge logaritmereglerne for at ændre venstresiden fra en addition og en subtraktion til en multiplikation og divition. Derefter indsætter vi basen 10 på begge sider av ligningen. 10 og log ophæver hinanden, så vi får 10x. på venstre side Til sidst deler vi med 10 for at finde x. Kontroller resultatet på lommeregneren |
b)
|
Først forenkler vi. Skriv begge sider som eksponenter af 10. |
c)
|
Forenkel først. Skriv begge sider som eksponenter af 10. |
d)
|
Forenkel først. Skriv begge sider som eksponenter af 10. |
|
lg (-5) existerer ikke |
Reglen log an = n log a bruges når man skal løse ligninger af typen ax = b, hvor eksponenten er den ukændte værdi.
Vi finder logaritmen til begge sider af lighedstegnet, og bruger ovennævnte regel for at flytte x foran logaritmen.
ax = b
lg ax = lg b
x lg a = lg b
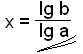
Løs
ligningen 2x = 8192. |
|
lg 2x = lg 8192 |
Find log til begge sider af ligningen |
x lg 2 = lg 8192 |
og flyt x foran log som nævnt i reglen. |
x = lg 8192/lg 2 = 13 |
Divider med log2 på begge sider af lighedstegnet for at finde x. |
Prøv test 2 i Eksponenter og Logaritmer.
Husk at bruge din tjekliste.