Fra algebraen, hvor vi ofte benytter potensregning, ved vi, at:
 a³∙ a² = a∙a∙a ∙ a∙a = a³⁺² = a⁵.  

Vi skal altså addere (lægge sammen) eksponenterne når flere potenser med samme rod multipliceres (ganges).

Her er et andet eksempel:

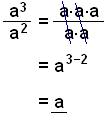
Dette viser os, at når en potens divideres med en potens med samme rod, gør man det modsatte af det vi gjorde i forrige eksempel. Ved division af potenser med samme rod, fås resultatet ved at beholde roden og trække eksponenten, der står i tælleren, fra eksponenten, der står i nævneren.

Regler:

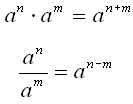
Her er to konkrete eksempler på brugen af regel nummer 2:

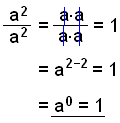
Her brugte vi to forskellige metoder, for at reducere udtrykket, og vi fik det samme svar. Som vi ser, bliver alle potenser hvor eksponenten er nul = 1

Næste eksempel viser, at en negativ eksponent er det samme som en positiv eksponent under brøkstregen.

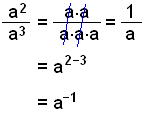
Regel:

Eksempel 1

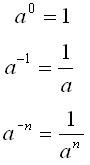
Reducer udtrykket og giv resultatet med positive eksponenter.

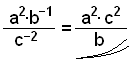Vi flytter b−1 ned, og ændrer den til b1= b. Så flytter vi c−2 op, og ændrer den til c2

Reducer udtrykket:

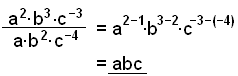Her bruger vi reglerne for multiplikation og division. At trække negative eksponenter fra hinanden, er det samme som at addere positive eksponenter med hinanden.

Reducer udtrykket, og giv resultatet med positive eksponenter:

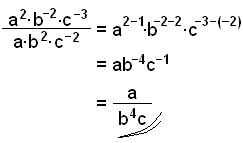
Nu skal vi se, hvad der sker, når vi opløfter tallene i en parentes.

    (a³b)² = (a∙a∙a∙b)∙(a∙a∙a∙b) = a^3∙2 b^1∙2 = a⁶b²

Hver faktor bliver opløftet med den eksponent som er parentesens eksponent.

Regel:

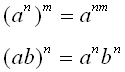
Her er eksempler på brugen af disse regler.

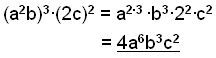Alle led inde i parenteserne opløftes med parentesens eksponent.  (b =b1 )

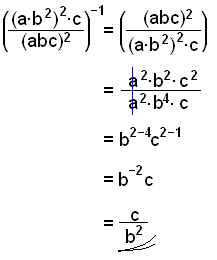Her kan vi ændre eksponenten -1 til 1 ved at vende brøken om, så tælleren bliver nævner og omvendt.

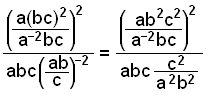	Først reducerer og fjerner vi den inderste parentes.
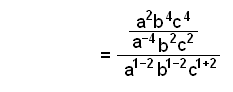	Så reducerer og fjerner vi de andre parenteser.
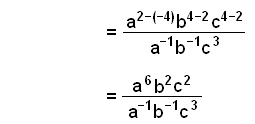	Derefter reducerer vi leddene i tæller og nævner.
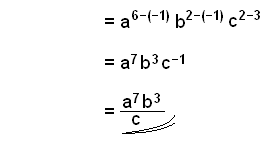	Så bruger vi reglerne for multiplikation og division til at forenkle hele udtrykket. Til sidst sørger vi for, at alle eksponenter er positive, ved at flytte de negative under brøkstregen.

Prøv nu test 1 i Eksponenter og Logaritmer.  

Husk at bruge tjeklisten.