Matematikhjælpen - Mængdelære - Intro 2

Mængdelære

Introduktion 2

Numeriske mængder

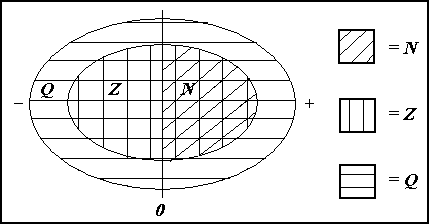
I matematikken findes der flere forskellige numeriske mængder (mængder af tal) Her er en skitse, som viser forholdet mellem dem.

Den enkleste mængde er mængden af naturlige tal. Taler man om denne mængde, bruger man altid bogstavet N.

N = { 1,2,3,∙∙∙ }. De naturlige tal er de tal, man bruger, når man tæller, og de fortsætter i det uendelige. Ofte indgår nul i mængden af naturlige tal, men så ændres symbolet til N_0.

N₀ = { 0,1,2,3,∙∙∙}.

Taler vi om mængden af hele tal, altså både de negative og de positive hele tal, bruger vi symbolet Z.

Z = { ∙∙−2,−1,0,1,2,∙∙ }.

Mængden N er en delmængde af mængden Z

N Z

Den tredje mængde, vi i denne omgang nævner, har symbolet Q. Det er mængden af rationelle tal, Altså mængde af alle brøker, som i både tælleren og nævneren har hele tal.

Bemærk: Alle hele tal kan skrives som brøker.

Derfor er både Z og N delmængder af Q.

Z Q och N Q

Du har nok bemærket, at alle elementer i disse tre mængder skrives med hele tal.

Hvad sker der, når vi bruger decimaltal ?


	Eksempel 1

Skriv

som decimaltal

Når vi beregner 1 divideret med 3, får vi

0,333∙∙∙∙

og 4 divideret med 33 bliver

0,1212∙∙∙∙

Decimaltallene i disse eksempler har et uendeligt antal decimaler efter kommaet. Den samme rækkefølge af decimaler gentager sig igen og igen. Sker dette taler vi om periodiske desimaler.

I første eksempel er perioden en decimal, nemlig tallet 3. I andet eksempel består perioden af to decimaler, hvor 1 og 2 gentager sig. Alle rationelle tal kan skrives som periodiske decimaler.

Disse eksempler viser, hvordan en brøk kan laves om til et decimaltal ved division.

Nu skal vi se, hvordan et decimaltal laves om til en brøk.

Hvis decimaltallet har et bestemt antal decimaler, kan vi kan vi lave det om til en brøk ved at flytte kommaet, indtil vi har et helt tal, og så dividere det med 10, 100, 1000… alt efter, hvor mange pladser vi flytter kommaet.

Eksempel 2

Skriv 0,3, 0,12 og 0,1212 som brøker.

0,3

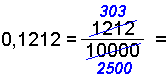Denne metode virker ikke når vi har med periodiske decimaltal at gøre, da de har et uendeligt antal decimaler efter komma. I sådanne tilfælde bruger vi en anden metode.

Eksempel 3

lav 0,333∙∙∙∙∙, 0,1212∙∙∙∙∙ og 1,14333∙∙∙∙ om til brøker

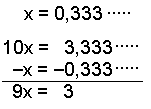Kald tallet for x. Når perioden består af en decimal, ganger vi tallet med 10, så vi får 10x.

Derefter trækker vi det første tal fra 10x.

På denne måden kommer vi af med decimalerne.

Til slut dividerer vi svaret med 9 på begge sider af lighedstegnet for at finde x.

Forkort, hvis det er muligt.

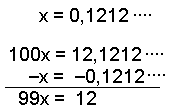Kald tallet for x. Denne gang har perioden to decimaler, så vi multiplicerer tallet med 100 og får 100x

Derefter trækker vi det første tal fra 100x.

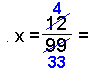
Igen kommer vi af med alle decimalerne

Til slutt dividerer vi svaret med 99 på begge sider af lighedstegnet for at finde x. Forkort,hvis det er muligt.

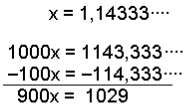I dette eksempel begynder vi med at multiplicere med 100 for at få perioden til at starter lige efter kommaet. (100x = 114,333..)

Perioden har derefter kun en decimal, så vi multiplicerer igen med 10, og får 1000x

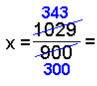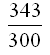Så trækker vi 100x fra 1000x, og kommer af med decimalerne.

Til slut dividerer vi med 900 på begge sider af lighedstegnet og forkorter for at finde x.

Prøv nu test 2 i mængdelære
Husk at skrive resultatet ind i din checkliste.