© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Funktioner I

Rationelle funktioner har følgende form:

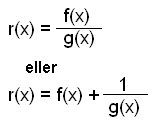
Da f(x) og g(x) både er flerleddede størrelser og nævneren, er g(x) mindst er af 1. grad (indeholdende et x).

Vi skal nu se på nogle rationelle funktioner och deres grafer.

Eksempel 1

Vi ser først på:

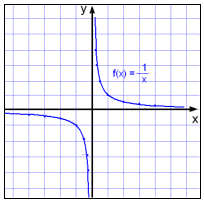
Starter vi med at udarbejde en værditabel (sildeben), opdager vi, at x ikke kan være 0, da man ikke kan dividere med 0.

Nærmer x sig 0, men fortsat er positiv ( x= 0.1 , x = 0.01  osv...), ser vi, at funktionsværdien (y-værdien) bliver større og større (eks. når x=0,01 så er y=100).

Nærmer x sig 0, men fra den negative side ( x= -0.1 , x = -0.01  osv...), ser vi, at funktionsværdien (y-værdien) får større og større negativ værdi(eks. når x=-0,01 så er y=-100).

Grafen til funktionen virker nærmest at være parallel med y-aksen jo nærmere den kommer x=0.

Når dette sker, er der tale om at funktionen har en lodret eller vertikal asymptote

(En lodret asymptote er en lodret linie, som funktionens graf nærmer sig mere og mere, når x går mod et fast punkt fra højre og/eller venstre)

Ligningen for asymptoten er x=0

Eksempel 2

Herefter vil  vi undersøge funktionen:

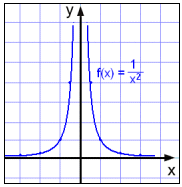
Vi ser, at funktionens værdier bliver større og større når x nærmer sig 0 fra højre (x > 0) og fra venstre ( x < 0 )

Også her er y-aksen en vertikal asyptot.

Vi lægger også mærke til at grafen hverken skærer x-aksen eller y-aksen.

Som et forsøg kan vi prøve at beregne disse skæringspunkter og se hvad der sker.

Vi finder ud af, hvor grafen skærer x-aksen ved at udregne f(0), da x-koordinaten for alle punkter på y-aksen er 0.

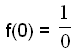
Skal vi udregne dette, må vi dividere med 0, hvilket er umuligt.

For at finde hvor grafen skærer x-aksen, må vi løse ligningen f(x) = 0 eller y = 0, for at alle punkter på x-aksen har y-koordinaten 0.

	= 0
1 = 0∙x2

Atter får vi en ligning, som ikke kan løses. Vi kan derfor konkludere, at grafen ikke skærer koordinatakserne.

Eksempel 3

Se på funktionen:

og kalkuler hvor grafen skærer akserne.

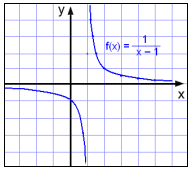
Hvis x = 1 kommer vi til at dividere med 0 og derfor må x ≠ 1. Når x nærmer sig 1 bliver y større og større, positivt når x>1 og negativt når x<1.

Denne gang ses grafen at ligge nærmere den linie, der går igennem x = 1 og og går opad når x > 1 og nedad når x < 1.

For at finde hvor grafen skærer y – aksen udregner vi f(0), da x = 0 på y – aksen.

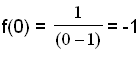
For at finde det punkt, hvor grafen skærer x-aksen løser vi ligningen f(x) = 0 eller y = 0 da alle punkter på x – aksen har y = 0.

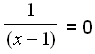
1 = 0∙(x − 1) = 0

På ny får vi en ligning, som ikke har nogen løsning, så vi kan konkludere, at grafen ikke skærer x-aksen

Eksempel 4

Se på funktionen

og find skærningspunkter på koordinatakserne

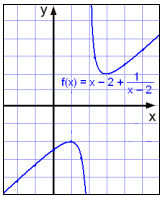
Vi konstaterer, at x ikke kan være 2 (x ≠ 2), da vi i så fald ville få 0 i nævneren. Når x ærmer sig 2 fra højre, bliver funktionsværdien større og større og grafen går opad. Nærmer x sig 2 fra venstre, får funktionen en større og større negativ værdi og grafen går nedad.

Så grafen har en vertikal asymptot x = 2

Grafen skærer y-aksen når x = 0

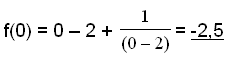
Grafen skærer y-aksen når f(x) = 0. Vi kan nu løse ligningen:

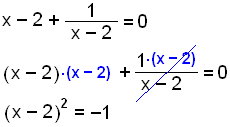Når vi multiplicerer på begge sider af lighedstegnet med (x - 2), får vi en ligning som ikke har nogen løsning.

Da ligningen f(x) ikke har nogen løsning skærer grafen ikke x-aksen.

Eksemplet ovenfor viser, at en rationel funktion næsten altid har en vertikal asymptot i punktet hvor nævneren er 0 (De eneste undtagelser er når vi kan faktorisere brøken og slette nævneren). Funktionen kan beregnes for alle andre x –værdier.

Exempel 5

Til sidst vil vi undersøge funktionen

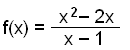
og finde den vertikale asymptot og grafens skæringspunkter i x- og y-aksen.

Start med at overveje: For hvilken x –værdi kan vi ikke udregne f(x)? Nævneren bliver 0, når x - 1 = 0; og det gør den, når x = 1.

Den vertikale asymptot er der hvor x = 1 og funktionen gælder for alle x-værdier med undtagelse af x = 1. Ved hjælp af mængde - betegnelsen kan vi skrive det som:

    {xÎR| x ¹ 1} eller R \ {1}

Find dernæst y-skæringspunktet ved et udregne f(0).

    f(0) = (0 − 0)/(0 − 1) = 0

Grafen skærer y-aksen i (0,0).

For at finde grafens skæringspunkt på x – aksen, må vi løse ligningen f(x) = 0.

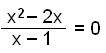x² − 2x = 0∙(x − 1) = 0

x(x − 2) = 0

x = 0 eller 2

Grafen skærer x-aksen i x = 0 og x = 2.

Prøv test 4 i funktioner 1.
Husk at overføre resultatet til din checkliste for at holde styr på hvor langt du er kommet.