Funktioner I
| © 2008 Rasmus ehf og Jóhann Ísak |
Funktioner I |
|
Lektion 3
Anden grads funktion
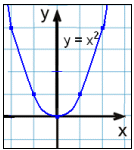
Lad os se på andengrads polynomier. Den mest enkle funktion er f(x) = x2. Grafen for denne funktion er en parabel.
 |
x | f(x) = x2 |
| -2 | (-22) = 4 | |
| -1 | (-12) = 1 | |
| 0 | (02) = 0 | |
| 1 | (12) = 1 | |
| 2 | (22) = 4 |
Vi kalder denne parabel for grundparabel eller basisgraf.
Læg mærke til, at grafen er symmetrisk i forhold til y-aksen. Y-aksen kaldes for symmetriaksen i denne funktion.
Efterfølgende skal vi se, hvordan koefficienterne påvirker grafens udseende.
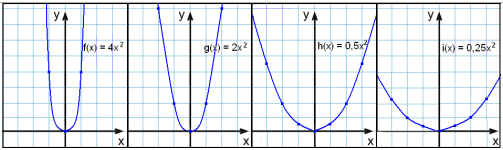
Koefficienten til x2 kalder vi som sædvanlig a. Indsætter vi forskellige værdier for a, så ser vi, at visse parabler er bredere og andre smallere end vores udgangsparabel, hvor a = 1
Her er grafer med parabler hvor a = 4, 2, ½ og ¼.
a = 4 a = 2 a = ½ a = ¼
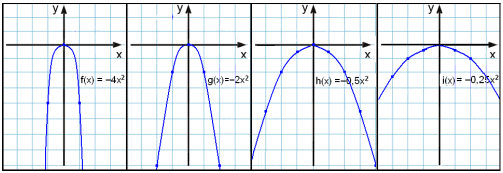
Her er parabler, hvor værdien for a er negativ.
a = −4 a = −2 a = −½ a = −¼
Hvis værdien af a er positivt, bøjer grafen sig opad (som et glad smiley). Jo størrer a- værdien bliver, jo smallere bliver grafen.
☺
Bliver a – værdien derimod mindre, vil grafen blive fladere og fladere indtil a-værdien bliver negativ, og grafen bøjer sig nedad (som en sur smiley)
L
Eksempel 1
Vi vil nu tegne grafen for f(x) = x2 + 1 og sammenligne den med g(x) = x2.
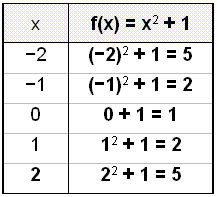 |
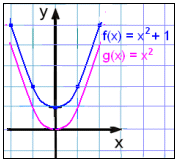 |
Y-værdierne for funktionen f(x) = x2 + 1 i værditabellen er alle en højere end de tilsvarende værdier i værditabellen for g(x) = x2 hvilket betyder at grafen er flyttet vertikalt op med 1 enhed.
Læg mærke til at grafen for f(x) = x2 + 1 ikke skærer x-aksen. Dette fortæller os, at ligningen x2 + 1 = 0 ikke har nogen løsning. Det ved vi, da et tal i ² aldrig er negativt; så x2 kan aldrig blive -1.
Eksempel 2
Tegn grafen for f(x) = x2 − 1 og sammenlign den med g(x) = x2.
 |
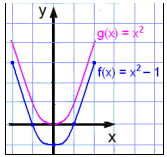 |
Nu er alle y-værdier i f(x)-tabellen en lavere end de tilsvarende værdier i tabellen for g(x) = x2 og grafen er flyttet vertikalt ned med 1 enhed.
Læg mærke til, at grafen for f(x) = x2 − 1 i dette eksempel skærer x-aksen to steder.
Dette betyder, at ligningen x2 − 1 = 0 har to løsninger,
x2 − 1 = 0
x2 = 1
x = ±1
hvilket er, at x = −1 og x = 1.
Eksempel 3
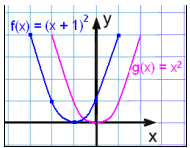
Tegn grafen for f(x) = (x + 1)2 ( eller f(x) = x2 + 2x + 1) og sammenlign den med grundparablen g(x) = x2.
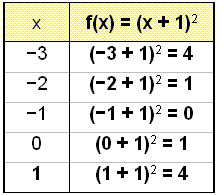 |
 |
Her har vi lagt 1 til x og vi kan se, at alle funktionsværdier i tabellen med samme værdi er flyttet en række op i sammenligning med basisfunktionen f(x) = x2
Grafen for f(x)= (x + 1)2 er den samme som grafen for g(x) = x2 , men vi flytter den en enhed til venstre.
Vi siger at basisgrafen er blevet forskudt med enheden -1 horisontalt. Symmetriaksen er nu x = -1.
Eksempel 4
Tegn grafen til f(x) = (x − 2)2 − 1 (eller f(x) = x2 − 4x + 3) og sammenlign den med basisgrafen g(x) = x2.
Anvender vi samme metode som i eksempel 3, kan vi forvente, at grafen flyttes to enheder til højre og en enhed nedad. Nu vil vi bevise det med en værditabel, og vi begynder med x = 0 og tegner så grafen.
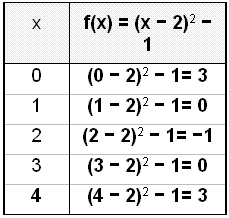 |
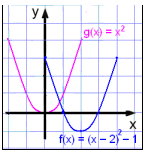 |
Læg mærke til, at symmetriaksen nu er x = 2.
Vi kan finde ud af, hvor grafen skærer y-aksen uden at tegne grafen. Vi gør det ved at beregne f(0) = 3 eller ved at reducere ligningen (x − 2)2 − 1 og ser da, at det konstante led (ledet uden x) er 3.
f(x) = (x − 2)2 − 1 = x2 − 4x + 4 − 1 = x2 − 4x + 3
eller f(0) = (x − 2)2 − 1 = 4 − 1 = 3
Eksempel 5
| (x − 2)2 − 1 = 0 | Flyt først -1 til den anden side af lighedstegnet. |
| (x − 2)2 = 1 | Derefter tager du kvadratroden på begge sider af ligningen. Husk både + og -. |
| x − 2 =
± |
Flyt til sidst 2 over på den anden side og vis resultatet. |
| x = 2 ± 1 |
Skæringspunkterne er x = 2 −1 = 1 og x = 2 + 1 = 3.
Vi ser, at skrives funktionen som f(x) = (x − 2)2 − 1 i stedet for som x2 − 4x + 3, så får vi mange informationer.
Det fortæller os, hvordan basisgrafen flyttes vertikalt og horizontalt
Det fortæller os også hvor symetriaksen placeres.
Og desuden kan vi på en let måde finde skæringspunkterne på x – og y – aksen.
Formlen for 2. gradsligningen er:
f(x) = a(x + r)2 + s
Som vi allerede har set, er a koefficienten til x2.
Symmetriaksen har ligningen x = −r (eller sagt med andre ord, at den har samme værdi som r, men med motsat fortegn).
Det er derfor vigtigt at vide, hvordan man omskriver funktionen
f(x) = ax2 + bx + c til formlen f(x) = a(x + r)2 + s
Eksempel 6
Vi vil nu se på, hvordan vi kan ændre en andengrads funktion fra en form til en anden, d.v.s ændre f(x) = x2 − 4x + 3 til f(x) = (x − 2)2 − 1.
Vi starter med den almindelige måde at skrive en andengrads ligning på:
f(x) = ax2 + bx + c
f(x) = x2 − 4x + 3
Her er a = 1
og b = −4
og c = 3 (så grafen skærer y-aksen ved 3).
Lad os se på reglen for kvadratet på en toleddet størrelse :
Vi ser at koefficienten for x er 2q.
I eksemplet f(x) = x2 − 4x + 3 er koefficienten af x -4, hvilket betyder at 2q = − 4 og derfor må q være −2.
Hvis vi udregner (x − 2)2 får vi x2 − 4x + 4, da
(x − 2)2 = x2 − 4x + 4.
Men trækker vi 1 fra, får vi:
(x − 2)2
−1 = x2 − 4x + 4−1 = x2 − 4x + 3
Med andre ord kan vi beskrive reglen som følger:
| f(x) = x2 − 4x + 3 | Den halve koefficienten af x er −4/2 = −2, som vi kvadrerer (4 ) og lægger til ligningen. |
| = (x2 − 4x + 22) − 22 + 3 | |
| = (x − 2)2 − 4 + 3 |
Lægger vi 4 til ligningen må vi også trække 4 fra så ligningen fortsat er uforandret. Vi udregner −4+3 = −1 |
| = (x − 2)2 − 1 |
Fra ovennævnte eksempel kan vi drage følgende slutning, nemlig at grafen til et anden grads polynom, hvor a = 1 (f(x) = x2 + bx + c) har sin symmetriakse i:
x = −b/2 og skærer y-aksen hvor y = c.
Eksempel 7
Find symmetriaksen til grafen for f(x) = 2x2 − 12x + 10.
I dette tilfælde er a = 2, så reglen fra eksempel 6 kan ikke bruges her.Det er heller ikke altid lige let at omskrive funktionen som nævnt ovenfor
I stedet flytter vi funktionen ned med 10 enheder ved at trække 10 fra i ligningen. At flytte grafen i vertikal retning ændrer ikke noget ved symetriaksens position.
Vi kalder denne nye funktion for g(x) og finder ud af, hvor g(x) skærer x-aksen.
2x2 − 12x = 0
2x(x − 6) = 0
Denne ligning har løsningen x = 0 Λ x =6, så grafen til g(x) skærer x-aksen i 0 og 6. Symmetriaksen må derfor skære x-aksen i x = 3.
Eksempel 8
Omskriv funktionen f(x) = 2x2 − 12x + 10 til formen f(x) = a(x + r)2 + s.
| f(x) = 2x2 − 12x + 10 | Lav en parentes uden om de to første led, og sæt to udenfor parentesen. Den halve koefficienten af x er −6/2 = −3, så plus med 32 inden i parentesen. Da vi nu har adderet 18 til indenfor parentesen, så må vi nu subtrahera 2×32 = 18 uden for parentesen. |
| = 2(x2 − 6x + 32) − 2∙32+ 10 | |
| = 2(x2 − 6x + 9) − 18 + 10 | |
| = 2(x − 3)2 − 8 |
Nu ser vi, præcis som i eksemplet før, at symmetriaksen går igennem x = 3.
Koefficienterne af x i eksemplet ovenfor (f(x) = 2x2 − 12x + 10) er: a = 2, b = −12 och c = 10. For at finde symmetriaksen, satte vi faktoren 2 udenfor parentesen. Dette modsvares ved at dividere med 2. Herefter tog vi kvadratet af denne toleddede størrelse ved at dele koefficienten af x (−6) med 2.
Den generelle formel for symmetriaksen til funktionen
f(x) = ax2
+ bx + c
er
derfor:
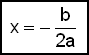
Hvilket også er x-værdien til parablens toppunkt.
Eksempel 9
Find toppunktet til parablen f(x) = 2x2 − 12x + 10.
Toppunktet ligger på symmetriaksen og derfor kender vi x-værdien for toppunktet (3).
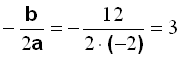
Vi finder y-værdien ved at udregne f(3). f(3) = 2∙32 − 12∙3 + 10 = 18 − 36 + 10 = −8.
Toppunktet til parablen f(x) = 2x2 − 12x + 10 er (3, −8).
Note 1: y-værdien kan også findes ved hjælp af formlen:
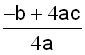
Note 2: Hvis a>0 så er toppunktet bunden af parablen. Hvis a<0 så er toppunktet toppen af parablen. ( se starten af denne lektion)
Prøv test 3 i funktioner 1.
Husk at overføre resultatet til din checkliste.