Funktioner
| © 2008 Rasmus ehf og Jóhann Ísak Pétursson |
Funktioner |
|
Her er nogle eksempler på polynomer:
| Grad |
f(x) |
Graf exempel: |
|
0 |
f(x)
= a Koefficient: a |
|
|
1 |
f(x)
= ax+b |
|
|
2 |
f(x)
= ax2+bx+c |
|
|
3 |
f(x)
= ax3+bx2+cx+d |
|
|
4 |
f(x)
= ax4+bx3+cx2+dx+e |
|
|
Osv. |
||
Koefficienterne a, b, c, osv., er kendte konstanter, som bestemmer formen af polynomiet. X er en variabel, som kan have forskellige værdier.
Den højeste potens af x, som er mulig for et polynom, kaldes polynomets grad.
Vi skriver udtrykket med den højeste potens af x først, derefter de andre i rækkefølge.
Hvis der mangler en potens af x, er det, fordi koefficienten er nul.
Hvis der mangler en koefficient foran et af leddene, er det, fordi koefficienten er 1.
Eksempel 1
Find graden og koefficientene til polynomiet
f(x) = x5 − 2x3 + 4x − 5
Den højeste potens til x er 5, så dette er et polynom af 5. grad.
x4 og x2 mangler, så deres koefficienter er 0. x5 har ingen synlig koefficient, så koefficienten er 1.
Vi kan tænke os, at leddet uden x er x0, da alle tal blir 1 i nulte potens. Nu kan vi skrive polynomiet på ny og notere koefficientene.
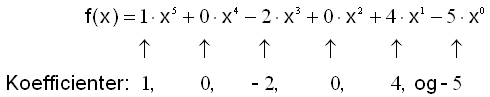
Læg mærke til, at et polynom i 5. grad har 6 koefficienter. Antallet af koefficienter er altid en mere end graden til polynomiet.
Potenserne i et polynom er altid hele, positive tal eller nul. (I mængden N0). De følgende funktioner er ikke polynomer.
|
f(x) = x2 + x + 1 + x−1 + x−2 |
(negativ potens af x) |
|
g(x) = x2 + x + 1 + Öx |
(x under et rodtegn) |
|
h(x) = x2 + x + 1 + 2x |
(x som potens) |
|
|
(x i nævneren) |
Ser du på polynomiernes grafer ovenfor, kan du konstatere at et polynom af 0. grad er en horisontal linie.
Grafen til et 1. grads polynom er en ret, skrå linie.
Grafen til et 2. grads polynom er en parabel. Den har et vendepunkt.
Grafen til et 3. grads polynom er næsten som 2 sammensatte parabler, den ene med åbning nedad, og den anden med åbningen opad. Den kan have to vendepunkter.
Grafen til et 4. grads polynom er som tre sammensatte parabler, med maksimalt 3 vendepunkter. Og sådan fortsætter det.
Øges polynomiet grad, øges antallet af mulige vendepunkter ligeledes. Det maksimale antal vendepunkter er altid én mindre end graden til polynomiet.
På samme måde skærer et 1. grads polynom x-aksen én gang, et 2. grads polynom krydser x-aksem maksimalt 2 gange, et 3. grads polynom maximalt 3 gange og så fremdeles.
(se endnu engang på graferne ).
Konstantleddet
uden x fortæller os hvor grafen skærer y-aksen. Dette skyldes at x= 0 på
y-aksen, og sætter vi x= 0 ind i ligningen, sidder vi tilbage med netop
konstantleddet uden x.
När f(x) = 2x3 + 3x2 + 4x + 6
f(0) = 2∙03 + 3∙02 + 4∙0 + 6 = 6
Grafen skærer y-aksen i punktet (0,6)
For alle punkter på x-akse gælder, at y=0, så vi kan finde ud af, hvor grafen skærer x-aksen, ved at sætte y = 0 og løse ligningen for x.
y = f(x) = 0.
All punkter på x-axeln har y-värdet noll så
att vi kan finna vart grafen skär x-axeln genom att sätta y = 0 och lösa
ekvationen för x. y = f(x) = 0.
Eksempel 2
Find de punkter, hvor polynomiet
f(x) = 2x + 4 skærer x-aksen og y-aksen.
| Skæringspunktet på y-aksen: 4. | Konstanten i formlen for f(x) er 4. |
|
Skæringspunktet på x- aksen: 2x + 4 = 0 |
Sæt f(x) = 0. |
|
2x = - 4,
x = −4/2, x = −2 |
Løs ligningen for at finde x. |
| Skæringspunktet på x- aksen er altså −2. |
Eksempel 3
Find skæringspunkterne til polynomiet f(x) = x2 − 2x på x- og y-aksen.
| Skæringspunktet på y-aksen er 0. | Konstanten i formlen for f(x) er 0. |
|
Skæringspunktet på x-aksen: x2 − 2x = 0 |
Sæt f(x) = 0. |
| x (x − 2) = 0 | Faktoriser og løs ligningen for at finde x. |
| Polynomet skærer x-aksen i to punkter, x= 0 og 2. |
Eksempel 4
Find skæringspunkterne til polynomiet
f(x) = (x − 1)(x − 2)(x − 3) på x- og y-aksen.
Undersøger vi ligningen, ser vi, at multiplicerer man parenteserne, bliver konstantledet -6.
Kan du ikke finde ud af det på denne måde, kan du finde konstanten ved at gange parenteserne med hinanden.
(x − 1)(x − 2)(x − 3) = (x2 − 2x − x + 2)(x − 3)
= (x2 −3x + 2)(x − 3)
= x3 − 3x2 − 3x2 + 9x + 2x − 6
= x3 − 6x2 + 11x − 6
En mere enkel måde at finde skæringspunktet på, er at udregne f(0) uden at gange parenteserne sammen.
f(0) = (0 − 1)(0 − 2)(0 − 3) = −6
Skæringspunktet på y-aksen er ved −6.
For herefter at finde ud af hvor grafen skærer x-aksen, skal vi løse følgende ligning
(x − 1)(x − 2)(x − 3) = 0
Den eneste måde, denne ligning kan få resultatet 0, er, hvis en af faktorerne (her parenteserne) blir 0. Dette sker når x = 1, 2 eller 3.
Derfor skærer grafen x-aksen når x=1, x=2 og x=3.
Eksempel 5
Ligger punkterne (1, 6) og (2, 8) på grafen til funktionen f(x) = x2 + 4x + 1.
| f(1) = 12 + 4∙1 + 1 |
Udregn f(1). |
| = 1 + 4 + 1 = 6 |
Punktet (1,6) er altså på grafen.
f(2) = 22 + 4∙2 + 1
= 4 + 8 + 1 = 13
Punktet (2,8) er altså ikke på grafen.
Eksempel 6
Find ligningen til det 1. grads polynom (den rette linje), som går gennem punkterne (1, 1) og (2, 3).
Funktionsforskriften for den rette linie er: f(x) = ax + b
| f(1) = a∙1 + b = 1 får vi ligningen a + b = 1 |
Når vi indsætter værdierne (1, 1): |
| f(2) = a∙2 + b = 3 får vi ligningen 2a + b = 3 |
Når vi indsætter værdierne (2, 3): |
|
f(2) − f(1) =
(2a + b) − (a + b) = 3 − 1 = 2a + b − a − b = 2 a = 2 2 + b = 1 b = 1 − 2 = −1 |
Løs ligningerne a + b = 1 og 2a + b = 3:
|
Ligningen til polynomet (den rette linien) er f(x) = 2x − 1.
Eksempel 7
Find et 2.grads polynom (en parabel), hvor grafen går igennem punkterne (0, 6), (1, 0) og (3, 0).
Kald funktionen f(x) = ax2 + bx + c og udregn a, b og c.
(0, 6) er skæringspunktet på y-aksen, så c = 6.
(1) = a∙12 + b∙1 + 6
| f(3) = a∙32
+ b∙3 + 6 = 0 = 9a + 3b + 6 = 0 3a + b + 2 = 0 |
Reducer ligningen ved at dele alle leddene med 3. |
f(3) = f(1) = 0
3a + b + 2 = a + b + 6
3a − a + b − b = 6 − 2
2a = 4
a = 2
f(1) = 2 + b + 6 = 0
b = −2 − 6 = −8
Derfor er polynomet f(x) = 2x2 − 8x + 6
Prøv test 2 i
Funktioner 1.
Husk at overføre resultatet til din checkliste.