Funktioner
| © 2008 Rasmus ehf og Jóhann Ísak |
Funktioner |
|
Funktioner og grafer
Eksempel 1
Vi ser på ligningen y = 2x + 4.
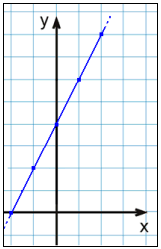
Først laver vi et skema (sildeben), hvor vi for hver x-værdi udregner y-værdien. Disse ordnede talpar (x,y), afsættes i et koordinatsystem, og der tegnes en ret linie igennem punkterne.
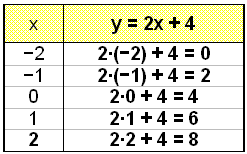 |
 |
Dette kan gøres meget let med en lommeregner, der kan lave grafiske kalkulationer. Har man en sådan lommeregner (Casio), vælger man TABLE i menuen.


I det skærmbillede, der fremkommer nu, skriver vi 2x + 4, så Y1 = 2x + 4.
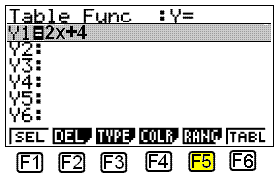
Når vælger vi, hvilke X – værdier vi vil bruge. Det gøres ved at vælge RANG, altså trykke på F5. Det giver os følgende skærmbillede.
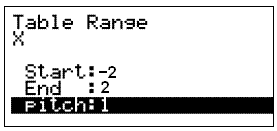
Vi vælger x-værdierne fra -2 til 2. Ved hjælp af ”PITCH” kan vi bestemme hvor stor afstanden skal være mellem de enkelte x-værdier. I dette tilfælde vælger vi, at afstanden skal være 1 og trykker så på EXE
Tryk på følgende knapper for at indtaste ovenstående:
![]()
Derved fremkommer det forrige skærmbillede. Vi vælger TABL. ved at trykke på F6. Nu fremkommer skemaet (sildeben) med ordnede talpar.
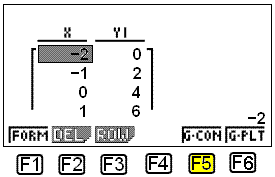
Lommeregneren tegner nu grafen på skærmen når vi vælger G-CON ved at trykke på F5
er det også muligt at lave et skema (sildeben) og tegne en graf.
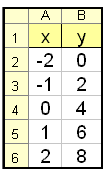
I EXCEL trykker vi tallene -2 och -1 ind i cellerne A2 och A3 (se EXCEL-tabellen nedenunder). Vi kan herefter automatiskt udfylde resten af A kolonnen ved at markere A2 og A3 og derefter kopiere nedad. Formlen i B2 er =2*A2 + 4 som kopieres.
|
Vi kan tegne grafen ved at markere tallene i de to kolonner og derefter trykke på diagramknappen (1). |
|
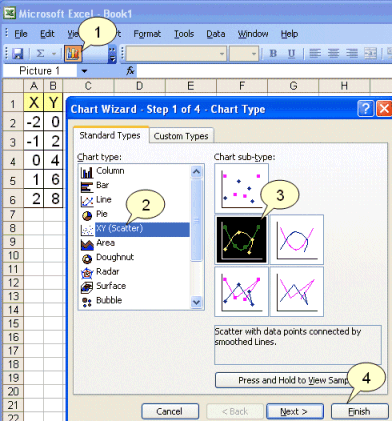 |
Vi vælger under diagramtyper ”XY-punkt” (2)
|
| og vælger derefter en af undertyperne (3) | |
| inden vi trykker på udfør (4).
|
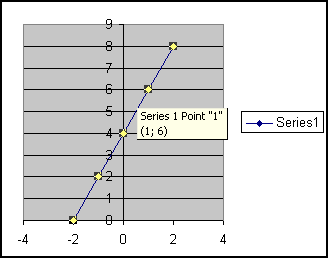
Vi kan ændre på grafernes udseende ved at højre klikke på det, vi vil forandre.
Eksempel 2
Lav et skema(et sildeben) og tegn grafen:
|
x = y |
|
 |
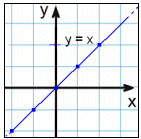 |
|
y = 2 |
|
 |
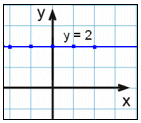 |
|
y = x2 |
|
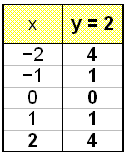 |
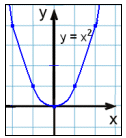 |
|
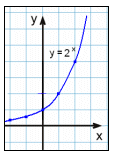
y = 2x |
|
 |
 |
Vi skal også se på
nogle opgaver, som ikke kan løses på denne måde, idet vi ikke kan bruge
tabelfunktionen på lommeregneren. Her skriver vi ikke y =, men: f(x) = ax² + bx
+ c.
Graf x = 2
Det vi ved, er at x = 2. Laver vi et skema (sildeben), nytter det ikke noget, at vi skriver x = 2 hele vejen. y kan have en hvilken som helst værdi, men vi vælger værdierne -2, -1, 0, 1 og 2.
Sådan vil skemaet (sildebenet) og grafen se ud|
|
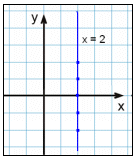 |
Resultatet er en vertikal linje igennem punktet 2 på x-aksen.
Eksempel 4
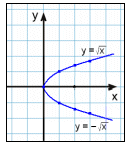
Vi vil nu se på ligningen y² = x.
Løser vi denne slags ligninger får y to svar, da
| y = ± |
|
Med andre ord findes der to værdier for y, for hver gang vi vælger et x. Vi kan kun vælge positive værdier for x, da det ikke er muligt at finde kvadratroden af et negativt tal.
Efterfølgende kan du se skemaet og grafen:
| X |
Y = ±
|
 |
| - 1 |
Umulighed |
|
| 0 | 0 | |
| 1 | ±1 | |
| 2 | ± 2 | |
| 3 | ± |
Eksempel 5
Vi vil nu se på ligningen x² + y² = 4
Løsningen er:
x2 + y2 = 4
y2 = 4 − x2
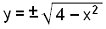
Også denne gang får vi to y-værdier for hver x-værdi vi vælger. Vi ser også at x-værdierne vi vælger, må være indenfor intervallet [−2, 2]. Ellers ville vi få et negativt tal under kvadratroden.
Efterfølgende ser vi skemaet (sildeben) og grafen
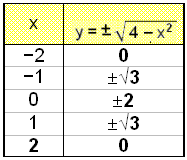 |
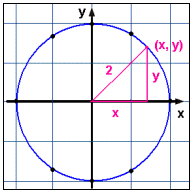 |
Sætter vi punkterne ind i et koordinatsystem, ser vi, at de danner en cirkel med centrum i origo (0,0). Radius for cirklen er 2.
Dette resultat er let at forklare, da x² + y² = 4 faktisk er den pythagoræiske læresætning for en retvinklet trekant, hvor hypotenusens længde er 2 og kateternes længde er henholdsvis x og y. Ovennævnte eksempler viser, at nogle ligninger kun har én y-værdi, for hvert x vi vælger, mens andre har to eller flere y-værdier for hvert x.
Ligninger, som forbinder et y med et x er meget vigtige i videnskaben og kaldes for funktioner. Man siger, at ”y er en funktion af x” og skriver det y = f(x) . Det læses som ”y er lige med f af x”.
I en funktion er der ingen talpar, der må have samme førstekomponent
Ser vi på den grafiske løsning af en funktion, opdager vi hurtigt, at en hvilken som helst vertikal linie vi tegner, kun skærer grafen én gang. Dette kan vi se på de eksempler vi har gennemgået.
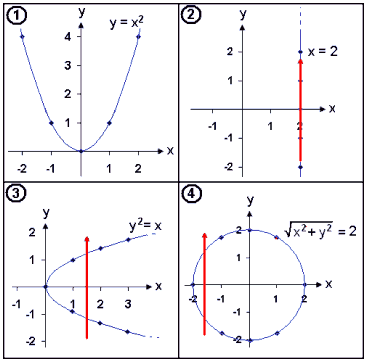
Den røde vertikale linie skærer graferne 2, 3 og 4 på to eller flere steder. Derfor er disse grafer ikke nogen funktionsgrafer. I eksempel 1 vil en vertikal linie, uanset hvor den placeres, skære grafen èt sted. Grafen er en funktionsgraf til ligningen y = x².
I stedet for at skrive ligningen som y=x², kan vi skrive den som f(x) = x², hvor y = f(x).
Vi bruger f(x) i stedet for y for at vise, at y-værdien afhænger af x-værdien, altså at y ”er en funktion af x”.
Hvis vi vælger x = 2, kan vi beregne y ved at sige: 2x² = 4.
Udtrykt matematisk siger vi, at ”f af 2 er ligemed 4.
Udtrykt på skrift vil der stå: f(2) = 2x² = 4.
Eksempel 6
| Givet funktion |
|
Find f(0), f(1) og f(3) |
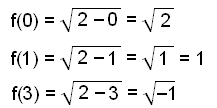 |
Vi indsætter værdierne 0, 1 og 3 i ligningen i stedet for x og udregner y værdien for hver funktion . | |
| Dette er umuligt | ||
På samme måde kan vi indsætte bogstaver i funktioner.
Hvis f(x) = x³ + x²
bliver for eksempel:
f(a) = a³ + a²
f(a²) = a6 + a4
f(a+1) = (a+1)³ + (a+1)².
Eksempel 7
Givet er funktionen: f(x) = x2. Find: f(a), f(2a), f(a+1) og f(a+b).
f(a) = a2
f(2a) = 4a2
f(a+1) = (a+1)2 = a2 + 2a + 1
f(a+b) = (a+b)2 = a2 + 2ab + b2
Prøv nu test 1 i funktioner 1
Husk at overføre resultatet til din checkliste.