© 2008 Rasmus ehf og Jóhann Ísak
Trekanter
|
© 2008 Rasmus ehf og Jóhann Ísak |
Trekanter |
|
Sinussetningen og cosinussetningen
I introduksjon 2 kom vi frem til regelen
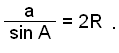
Denne regelen gjelder også hvis vi bruker vinkel B og side b, eller vinkel C og side c.
Derfra kan vi komme frem til sinussetningen:
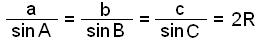 |
Vi kan bruke setningen til å finne ukjente vinkler og sider i en trekant, når vi vet en vinkel og den motsatte siden, i tillegg til en hvilken som helst side eller vinkel.
Sinussetningen brukes blant annet i landmåling og når man lager kart. Vi kan skrive om regelen på tre måter etter hvilke sider og vinkler som er ukjente.
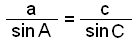 |
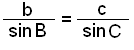 |
Tegningen under viser den samme trekanten vridd på tre forskjellige måter. Vi skriver opp formelen for arealet, og bruker forskjellig grunnlinje og høyde for hver gang.
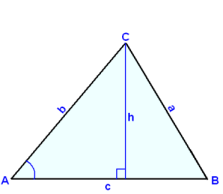 |
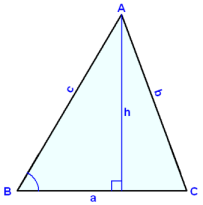 |
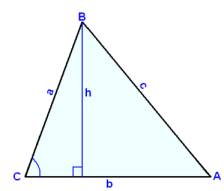 |
F = ½∙c∙h F = ½∙a∙h F = ½∙b∙h
Ved hjelp av regelen sin x = motstående katet/hypotenus får vi
sin A = h/b sin B = h/c sin C = h/a
h = b∙sin A h = c∙sin B h = a∙sin C
Arealet av trekanten er derfor:
| F = ½ ∙c∙b∙sin A F = ½∙a∙c∙sin B F = ½∙b∙a∙sin C |
Arealet F er selvfølgelig det samme hver gang, og vi kan bruke disse formlene til å skrive opp sinussetningen på en annen måte. Vi deler alle leddene på ½∙a∙b∙c.
½∙b∙c∙sin A = ½∙a∙c∙sin B = ½∙a∙b∙sin C = F
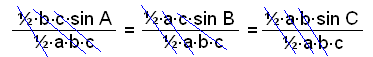
Og kommer frem til sinusregelen slik man vanligvis skriver den:
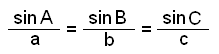 |
En spissvinklet trekant har sidene a = 12 cm, c = 13 cm og vinkel A = 60°. Finn vinkel C, side b og arealet av trekanten.
Først tegner vi en hjelpefigur.
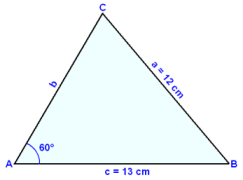
Deretter finner vi vinkel C ved hjelp av sinussetningen.
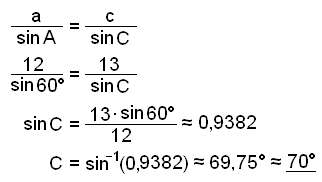
B ≈ 180° − 69,75° − 60° ≈ 50,25° ≈ 50°
Så finner vi b på samme måte.
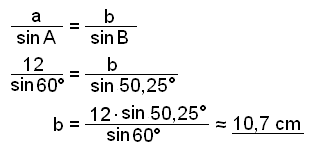
Til slutt finner vi arealet F ved hjelp av formelen for arealet av en trekant.
F = ½∙b∙c∙sin A ≈ ½∙10,7∙13∙sin 60° ≈ 60 cm2
En stumpvinklet trekant har sidene a = 12 cm, c = 13 cm og vinkel A = 60°. Finn vinkel C, side b og arealet av trekanten.
Denne trekanten er lik som den forrige, bortsett fra at trekanten inneholder en stump vinkel
( større enn 90°).
Da vi fant vinkel C i eksempel 1 over, gikk vi ut fra at kalkulatoren ga oss det riktige svaret. Utregningene var slik
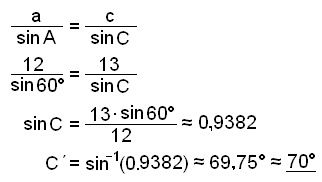 |
sinC = 0,9382 |
Siden denne trekanten har en stump vinkel, må vi huske på regelen som gir den andre løsningen på likningen. Regelen er slik:
sin v° = sin (180° − v°)
Dette
gir oss den stumpe vinkelen
C ≈ 180° − 70°
≈ 110°
og
dermed blir vinkel
B ≈ 180° − 60° −
110° ≈ 10°
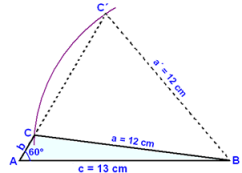
Men hvordan kan vi forklare at det kan være to forskjellige trekanter med de samme oppgitte målene? Se på tegningen under.
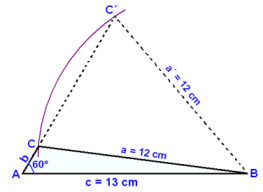
Først tegner vi grunnlinjen c = 13 cm. Vi tegner en vinkel på 60° på den ene enden av grunnlinjen, og kaller den A. Vi kaller den andre enden av grunnlinjen B. Vi bruker B som sentrum, og tegner en sirkel med radius 12 cm. Sirkelen skjærer vinkel A på to steder, og viser at punkt C kan være på to forskjellige steder. Den ene plasseringen gir en stumpvinklet trekant, den andre gir en spissvinklet trekant (se tegningen).
Nå skal vi fortsette med eksempel 2 og finne siden b.
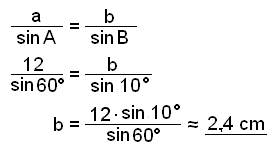
Til slutt regner vi ut arealet av trekanten.
F = ½∙b∙c∙sin A ≈ ½∙2,4∙13∙sin 60° ≈ 13,5 cm2
En stumpvinklet trekant har sidene a = 15 cm, c = 6 cm og angle A = 60°. Finn vinkel C og side b.
Tegn en hjelpefigur.
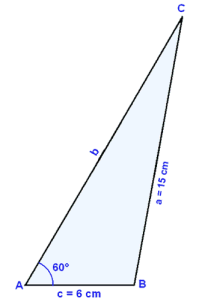
Bruk sinussetningen.
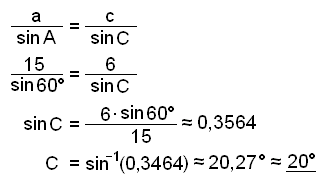
B ≈ 180° − 60° − 20,27° ≈ 99,73° ≈ 100°
Finn side b.
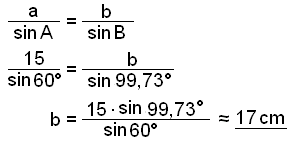
Disse utregningene stemmer med tegningen. Det finnes ingen annen trekant med de oppgitte målene.
Fra eksemplene ovenfor kan vi trekke følgende konklusjon:
|
Når siden rett overfor av den oppgitte vinkelen er kortere enn den hosliggende siden (grunnlinjen) må vi vite om vinkelen er spiss eller stump. Hvis vi ikke får oppgitt dette, er det to mulige trekanter, og dermed to riktige løsninger. |
Trekanten ABC har siden c = 12 cm og vinklene A = 60° og B = 80°. Finn sidene b og c.
Tegn en hjelpefigur med c = 12 cm som grunnlinjen. Vi kan lett finne den tredje vinkelen i trekanten, og når vi vet alle vinklene er det bare en mulig løsning.
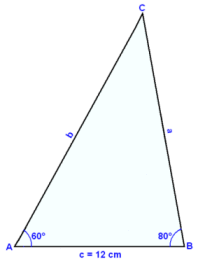
Først må vi finne vinkel C.
C = 180° − 60° − 80° = 40°
Så bruker vi sinussetningen til å finne siden a.
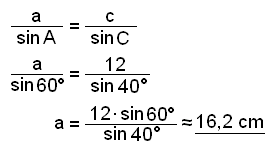
Til slutt finner vi siden b.
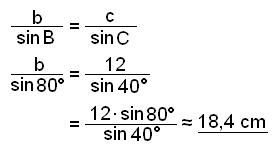
Vi kan alltid bruke sinussetningen til å finne ukjente sider og vinkler i entrekant hvis vi har oppgitt en side og to vinkler (se eksempel 4).
Vi kan også bruke sinussetningen hvis vi vet to sider og vinkelen rett overfor en av sidene (se eksempel 1-3). Men da må vite om trekanten er spissvinklet eller stumpvinklet.
Men hva om vi kjenner to sider og vinkelen mellom dem, eller bare tre sider og ingen vinkler?
Vi kan lett tegne opp en trekant med denne informasjonen, og dermed burde det også være mulig å regne ut de ukjente vinklene og sidene. Sinussetningen virker ikke, så vi må finne en annen metode.
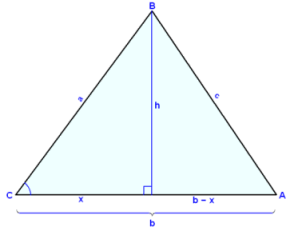
Vi tegner en trekant og deler den inn i to rettvinklede trekanter ved å tegne inn høyden. Så bruker vi Pythagoras på begge trekantene.
h2 = a2 − x2 og h2 = c2 − (b − x)2 = c2 − b2 + 2∙b∙x − x2
Vi setter likningene inn i hverandre og får:
c2 − b2
+ 2∙b∙x − x2 = a2 − x2
Så løser vi likningen for å finne c2.
c2 = a2 + b2 − 2∙b∙x
For å
bli kvitt
x,
bruker vi regelen
cos C = x/a som gir
x = a
cos C.
Når
vi setter dette inn for x, får vi:
| c2 = a2 + b2 − 2∙b∙a∙cos |
Denne formelen kalles cosinussetningen, og kan brukes til å finne siden c hvis vi vet sidene a og b, og vinkelen mellom dem (se tegningen over).
Vi kan bevise at cosinussetningen også gjelder for stumpvinklede trekanter. Beviset er veldig likt beviset for spissvinklede trekanter.
Hvis vi bruker andre vinkler og sider, får vi disse formlene:
| a2 = b2 +
c2 −
2∙b∙c∙cos
A
b2 = a2 + c2 − 2∙a∙c∙cos B |
Hvis vi kjenner alle sidene i en trekant, kan vi bruke cosinussetningen til å finne vinklene. Hvis vi for eksempel vil finne vinkel C, løser vi bare likningen og bruker en kalkulator til å finne vinkelen.
c2 = a2 + b2 − 2∙b∙a∙cos C
2∙b∙a∙cos C = a2 + b2 − c2
Når vi deler på 2ab, får vi dette:
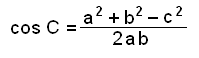 |
For de andre vinklene gjelder:
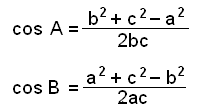 |
Trekant ABC har sidene c = 12 cm og b = 15 cm. Vinkel A, som er mellom sidene b og c, er 60°. Finn side a, vinkel C og arealet av trekanten.
Først tegner vi en prøvefigur.
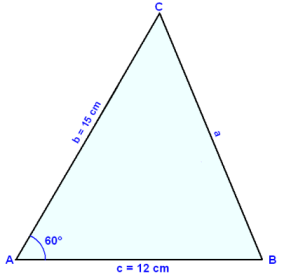
Vi finner cosA ved hjelp av cosinussetningen.
a2 = b2 + c2 − 2∙b∙c∙cos A
= 152 + 122 − 2∙15∙12∙cos 60°
= 225 + 144 − 180 = 189
![]()
Nå kan vi enten bruke sinussetningen eller cosinussetningen for å finne vinkel C. Her velger vi å bruke sinussetningen.
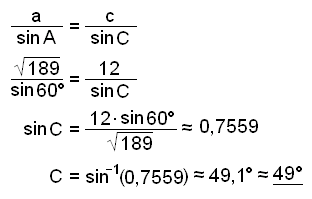
Til slutt finner vi arealet.
F = ½∙b∙c∙sin A ≈ ½∙15∙12∙sin 60° ≈ 78 cm2
Trekant ABC har sidene a = 12 cm, b = 11 cm og c = 13 cm. Finn arealet av trekanten.
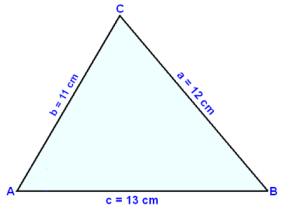
Før vi kan finne arealet, må vi finne en vinkel. Vi bruker cosinussetningen til å finne vinkel C.
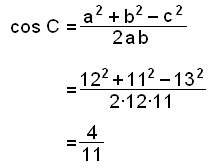 |
| C = cos-1(4/11) |
| C ≈ 68,7° |
Nå kan vi finne arealet av trekanten.
F = ½∙a∙b∙sin
C ≈ ½∙12∙11∙ sin 68,7° ≈ 61,5 cm2
Prøv Test 1 i Trekanter.
Husk å bruke sjekklisten.