© 2008 Rasmus ehf og Jóhann Ísak
© 2008 Rasmus ehf og Jóhann Ísak |
Trekanter |
|
Når en rett linje treffer en sirkel bare en gang, kalles den tangenten til sirkelen. Vinkelen mellom radiusen og tangenten i skjæringspunktet er alltid 90°.
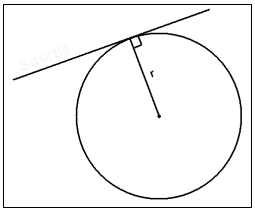
Vi tegner en rett linje som deler en vinkel i to like deler. Alle punktene på linjen er like nærme begge sidene i vinkelen. Hvis vi tegner en sirkel som blir tangert av sidene i en vinkel, er sentrum i sirkelen på linjen.
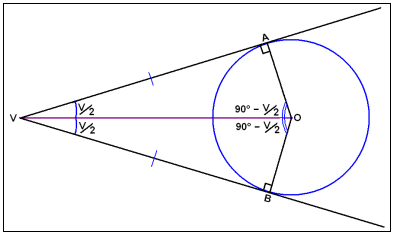
På tegningen over blir vinkelen V delt i to av linjen fra V til O. VA og VB er like lange, og vinkelrett på henholdsvis AO og BO.
I tegningen under er vinkelen V = 40°, og linjestykkene VA og VB er 40 cm. Finn vinkelen AOB, som er merket x, og radiusen i sirkelen.
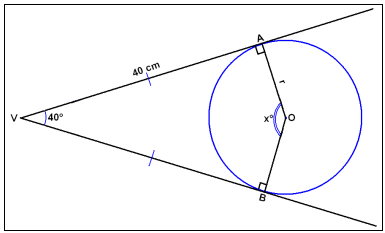
VAOB er en firkant, og summen av vinklene er derfor 360°. Vi kjenner allerede tre av vinklene, og kan regne ut den siste.
x° = 360° − 90° − 40° − 90° = 140°
Hvis vi tegner en linje VO, får vi en rettvinklet trekant med vinklene 20°, 90° og 70°. Vi bruker trigonometri, og får:
tan 20° = r/40
r = 40∙tan 20° ≈ 14,6 cm
Siden på motsatt side i forhold til vinkelen, forminskes med samme forholdstall som linjestykkene inntil vinkelen.
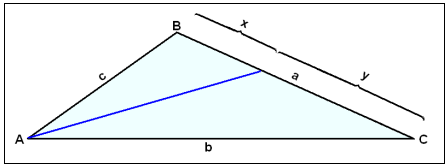
Linjen som deler vinkel A i to, deler opp siden a i forholdet c/b. Hvis vi kaller de to delene x og y, gjelder denne regelen:
![]()
Trekant ABC har følgende mål:
a = 30 cm, b = 40 cm og c = 20 cm.
Side a deles inn i to deler av den samme linjen linjen som deler vinkel A i to. Regn ut lengden av disse delene. Vi skriver på samme måte som i formelen over.
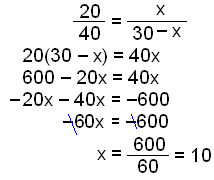
Side a deles inn i deler med lengdene 10 cm og 30 − 10 = 20 cm.
Hver trekant har et punkt som er like langt fra alle sidene i trekanten. Dette er punktet hvor linjene som deler hver vinkel i to, krysser hverandre. Vi bruker dette punktet som sentrum, og tegner en sirkel som tangeres av alle sidene i trekanten. Dette kalles en sirkel innskrevet i en trekant.
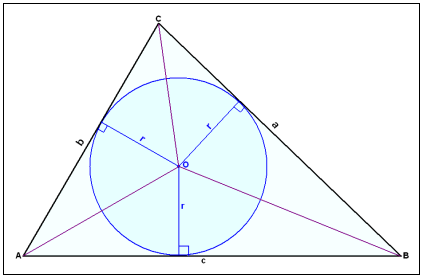
Vi kan se på tegningen at linjene AO, BO og CO deler trekanten inn i tre mindre trekanter, som alle har høyden r. Arealene deres er ½∙a∙r, ½∙b∙r og ½∙c∙r.Det totalet arealet av trekant ABC er derfor:
F = ½∙a∙r + ½∙b∙r + ½∙c∙r = ½∙r(a + b + c)
Vi kaller omkretsen til trekanten for u. u = a + b + c, og vi kan altså skrive formelen for arealet av trekanten som
![]()
Et annet punkt er like langt fra alle vinklene i trekanten. Tegner vi en sirkel gjennom alle vinklene i trekanten, blir dette punktet sentrum i sirkelen. En slik sirkel kalles en omskrevet sirkel.
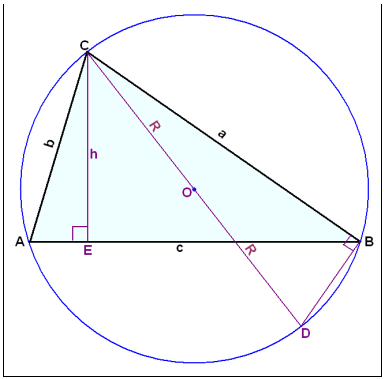
Tegningen over viser trekanten ABC med en slik sirkel. Vi har tegnet inn to rettvinklede trekanter. Vi fikk trekant ACE ved å tegne inn høyden h fra vinkel C ned på grunnlinjen c. Trekanten ACE fikk vi ved å tegne inn diameteren fra C gjennom sentrum O til et punkt D på den andre siden. Trekantene ACE og BCD er formlike, fordi de begge er rettvinklede, og fordi vinkel A = vinkel D. Vi får derfor disse forholdene:
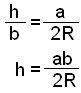
Når vi setter inn verdien h i formelen for arealet F av en trekant F = ½∙c∙h får vi at:
![]()
Vi kan også bruke dette:
![]()
Som kan omformes til regelen:
![]()
Hvis vi setter verdien h = b∙sin A inn i formelen for arealet F = ½∙c∙h finner vi formelen for arealet av trekanten:
F = ½∙b∙c∙sin A
En trekant har sider på 17 cm, 17 cm og 16 cm.
a) Finn arealet av trekanten.
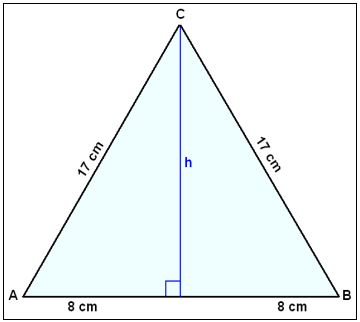
Bruk Pythagoras for å finne høyden.
h2 + 82 = 172
h2 = 289 − 64 = 225
h = 15 cm
Nå kan vi regne ut arealet F.
F = ½∙16∙15 = 120 cm2
b) Finn radiusen til den innskrevne sirkelen.
Omkrets u = 17 + 17 + 16 = 50 cm.
F = 120 = ½∙r∙50
r =120∙2/50 = 4,8 cm
c) Finn radius den omskrevne sirkelen rundt trekanten.
Areal F = 120 = 17∙17∙16/4R
480R = 17∙17∙16
R = 17∙17∙16/480 = 289/30 ≈ 9,6 cm
d) Finn vinklene i trekanten.
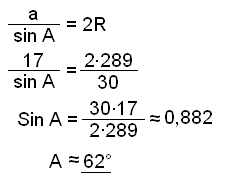
Da vet vi også at B ≈ 62° og C ≈ 180 − 2∙62 ≈ 56°.
Medianen i en trekant er et linjestykke tegnet fra en av vinklene til midtpunktet på den motsatte siden. Medianene i en trekant møtes i et skjæringspunkt. Dette punktet deler opp medianen i to like deler.
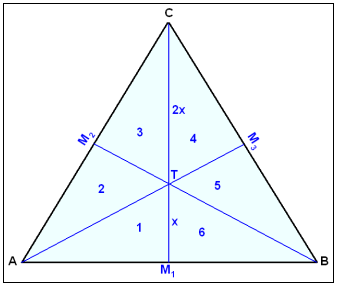
I tegningen over er M1, M2 og M3 midtpunktene på sidene i trekanten. Medianene møtes i punktet T, som deler M1C inn i delene x og 2x.
Medianene deler trekanten inn i seks mindre trekanter, nummerert 1-6 i tegningen. Disse trekantene har samme areal. Punktet T er derfor tyngdepunktet til trekanten. Hvis vi skulle balansere trekanten på en nål, måtte vi altså ha plassert den i T.
I en likesidet trekant er sentrum i den innskrevne sirkelen og sentrum i sirkelen rundt i samme punkt.
Medianene i en trekant krysses i et punkt.
Høydene i en trekant krysses også i et punkt.
Lengden av medianen i en trekant er 24 cm. Regn ut lengden av linjestykkene som de andre medianene deler den inn i.
Vi kaller den ene delen for x, og den andre for 2x.
x + 2x = 24
3x = 24
x = 8
Medianen deles inn i biter på 8 cm og 16 cm
En trekant ABC tegnes inn i et
koordinatsystem.
A = (−4, −4), B = (12, 0) og C = (4, 16). Finn koordinatene til punktet hvor
medianene møtes.
Vi begynner med å finne midtpunktet på siden BC.
![]()
Så finner vi likningen til medianen gjennom A, altså en linje gjennom A = (−4, −4) og (8, 8).
Stigningstallet k = (8 + 4)/(8 + 4) = 1
Vi bruker likningen for en rett linje på formen:
y = k(x − x1) + y1
y = 1(x − 8) + 8
y = x
Deretter gjør vi det samme med medianen gjennom B. Først finner vi midtpunktet på AC.
![]()
Vi har funnet likningen for medianen gjennom B. Den går gjennom B= (12, 0) og (0, 6).
Stigningstallet k = (0 − 6)/(12 − 6) = −½
Derfor er y = −½(x − 0) + 6
y = −½x + 6
Når vi løser de to likningene y = x og y = −½x + 6.
x = −½x + 6
x + ½x = 6
1½x = 6
x = 4 Da blir også y = 4
Medianene møtes i punktet (4, 4).
Denne regelen er oppkalt etter den italienske matematikeren Giovanni Ceva:
Vi tegner tre tilfeldige linjer i en trekant, hvor alle linjene går gjennom det samme punktet P og en vinkel i trekanten. Vi kaller punktene hvor de skjærerer sidene AB, AC og BC, for X, Y og Z.
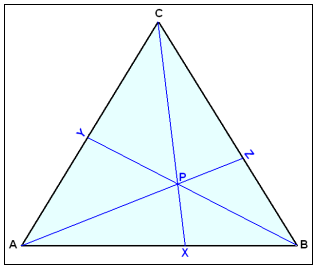
Da vil alltid:
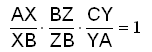
Denne regelen gjelder for medianer, høyder og alle andre linjer som går fra en vinkel til den andre siden, og møtes i et punkt.
Finn lengden av linjestykkene som Z deler BC inn i på tegningen under.
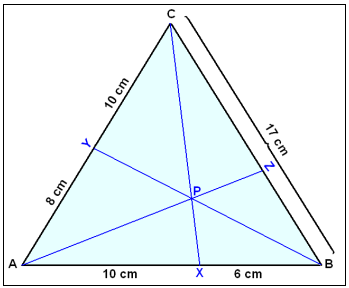
Hvis x = BZ, blir ZC = 17 − x. Vi bruker regelen og får at:
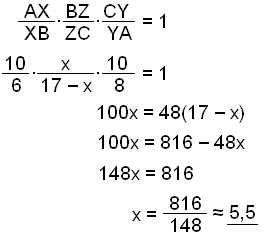
Derfor deler Z BC inn i linjestykker på 5,5 cm og 11,5 cm.
Prøv Test 2 i Trekanter.
Husk å bruke sjekklisten.