© 2007 Rasmus ehf og Jóhann Ísak
|
© 2007 Rasmus ehf og Jóhann Ísak |
Likninger III |
|
Introduksjon 3 Skjæringspunkter på grafer
Hvordan kan vi finne ut hvor to grafer y = f(x) og y = g(x) krysser hverandre?
Vi vet allerede hvordan vi kan finne ut hvor grafen f(x) skjærer x-aksen. På x-aksen vet vi alltid at y = 0, og vi finner skjæringspunktene ved å løse likningen f(x) = 0 .
Når to grafer y = f(x) og y = g(x) krysser hverandre, har de nøyaktig samme verdier av x og y i skjæringspunktene. Derfor kan vi finne skjæringspunktene ved å løse likningen f(x) = g(x). Løsningen vil gi oss x – verdiene til skjæringspunktene. Så kan vi finne y – verdiene ved å sette inn x – verdiene i en av likningene.
Eksempel 1
Finn skjæringspunktet mellom linjene f(x) = 2x − 1 og g(x) = x + 1. Først ser vi på grafen til de to funksjonene. Vi ser at skjæringspunktet er (2, 3).
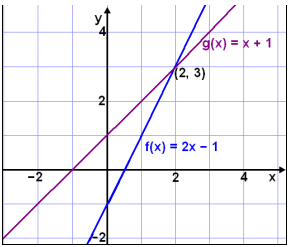
Vi finner skjæringspunktet ved regning ved å sette opp likningen f(x) = g(x):
2x − 1 = x + 1
2x − x = 1 + 1
x = 2
Vi finner y – koordinaten ved å regne ut f(2):
f(2) = 2∙2 − 1 = 3
Skjæringspunktet er (2, 3).
Eksempelet viser at vi kan finne skjæringspunktet på to forskjellige måter. Enten grafisk, ved å tegne to grafer i samme koordinatsystem, eller ved regning, ved å sette likningene for grafene lik hverandre.
Å løse en likning grafisk er lettere hvis man har en grafisk kalkulator, eller et dataprogram som Excel. Noen likninger må løses på denne måten.
Eksempel 2
Løs likningen x2 − 2x − 3 = 2x − 3. både grafisk og ved regning
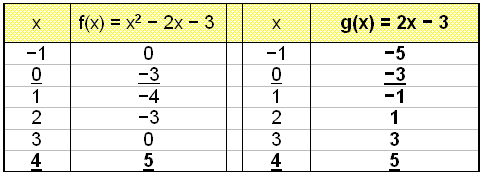
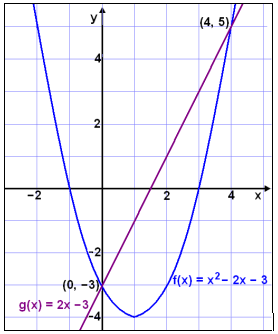
Vi tegner grafene til f(x) = x2 − 2x − 3 og g(x) = 2x − 3 ved å lage en verditabell og merke av punktene i et koordinatsystem. Vi ser, både på grafen og verditabellen, at grafene krysser hverandre når x = 0 og når x = 4.
Løst ved regning:
x2 − 2x − 3 = 2x − 3
x2 − 4x = 0
x(x − 4) = 0
Dette gir løsningene x = 0 eða x = 4.
Eksempel 3
Løs likningen x2 − 1 = 2x − 3
Først flytter vi alle leddene over til venstre side av likhetstegnet og forenkler.
Dette gir x2 − 2x + 2 = 0
Vi bruker abc – formelen med a = 1, b = −2 og c = 2.
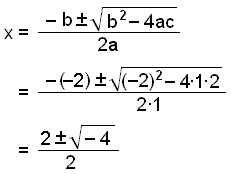
Tallet under rottegnet er negativt, og likningen har derfor ingen løsning. For å finne ut hvorfor, tegner vi grafene til hver side av likningen vi begynte med.
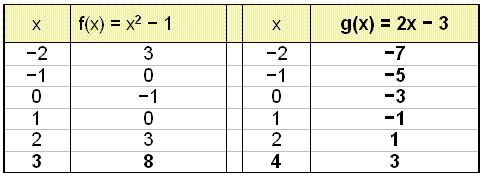
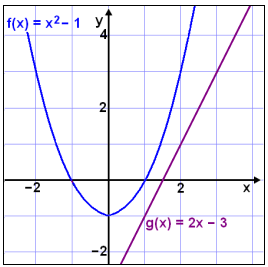
Vi ser at parabelen f(x) og den rette linjen g(x) ikke krysser hverandre. Vi kan ikke regne ut skjæringspunktet når det ikke finnes noe skjæringspunkt..
Eksempel 4
Løs likningen x3 − 3x + 2 = x2 − 2x + 1
Som sist flytter vi alle leddene over til venstre side.
x3 − 3x + 2 = x2 − 2x + 1
x3 − x2 − x + 1 = 0
(x3 − x2) − (x − 1) = 0
x2(x − 1) − (x − 1) = 0
(x − 1)(x2 − 1) = 0
(x − 1)(x − 1)(x + 1) = 0
Ved regning finner vi bare to løsninger, x = 1 og x = -1, selv om en tredjegradslikning kan ha opp til tre løsninger. Grafen viser hvorfor det bare er to.
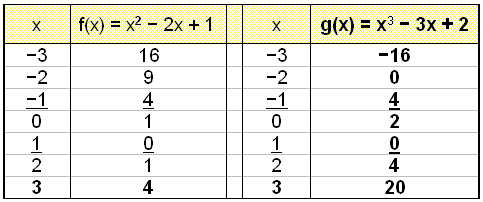
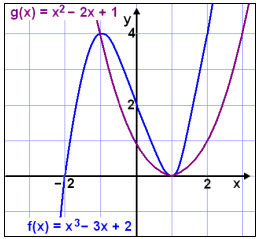
Grafene til f(x) = x2 − 2x + 1 og g(x) = x3 − 3x + 2 skjærer hverandre i bare to punkter, x = −1 og x = 1.
Eksempel 5
Løs
likningen x2 =
![]() x
x
Vi ser fort at x = 0 og x = 1 er løsninger er to av løsningene. Men finnes det flere løsninger? Det er ikke veldig sannsynlig, men vi skal se på grafene for å finne det ut.
Vi kaller venstre side
f(x) = x2 og høyre side g(x) =
![]() x.
g(x) kan ikke være negativ, så det kan ikke være noen negative skjæringspunkter.
x.
g(x) kan ikke være negativ, så det kan ikke være noen negative skjæringspunkter.
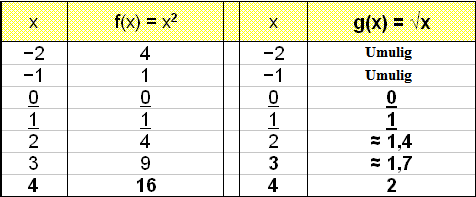
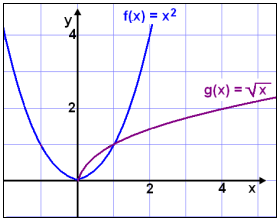
Grafen viser bare to skjæringspunkter.
Likningen har derfor bare to løsninger, x = 0 and x = 1.
Slik løser man likningen ved regning:
|
x2 =
x4 = x x4 − x = 0 x(x3 − 1) = 0 |
Kvadrer begge sider for å bli kvitt rottegnet. |
Dette gir løsningen x = 0 og x = 1.
Eksempel 6
Løs likningen ln x = x2 − 1
Denne likningen er ikke så enkel. Ved hjelp av definisjonen av logaritmer, ser vi at x = 1 gjør at begge sider blir 0. Dette er altså en av løsningene. Vi tegner grafer for å se om det finnes flere løsninger.
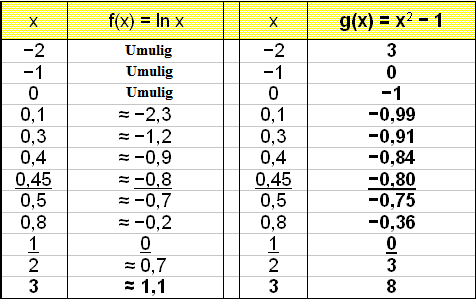
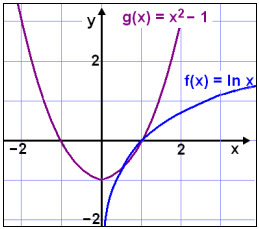
Grafene viser at det finnes to løsninger. En løsning er x = 1 fordi e0 =1.
Merk at vi velger x – verdier for at y – verdiene skal komme nærmere og nærmere hverandre i verditabellen. På denne måten kan man velge x – verdier ut fra hvor nøyaktig svar man ønsker.
|
Eksempel 7 |
|
EXCEL |
Det er mye lettere å løse likningen ln x = x2 − 1 på en grafisk kalkulator.
Vi tegner opp grafene av begge sider av likningen, og bruker ”Zoom” (shift F2) og ”Trace” (shift F1) for å finne skjæringspunktet.
Det er enda lettere å bruke ”G-Solve” (F5) og funksjonen som finner skjæringspunkter, ”ISCT” (F5). Dette gir oss det første skjæringspunktet. For å finne det andre, trykker vi på høyrepilen, og kalkulatoren gir oss det andre skjæringspunktet.
I EXCEL kan vi bruke ”målsøking” til å løse likninger som er vanskelige å løse ved regning.
Først setter vi opp likningen slik:
ln x = x2 − 1
1 = x2 − ln x
Det første vi gjør er å velge en x – verdi, og skrive den inn i celle B2. Her har vi valgt 0,1. Så skriver vi formelen for høyre side av likningen, x2 − ln x , i D2.
Formelen ser slik ut i EXCEL:
= B2^2−ln(B2)
Velg ”Verktøy” / "Tools" og deretter ”Målsøking” / "Goal Seek".
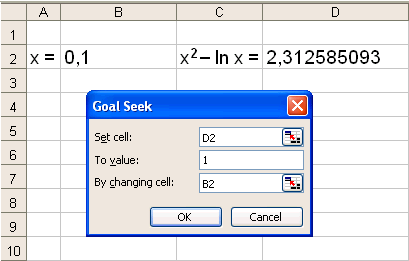
Vi skriver D2, 1 og B2, og EXCEL vil gjøre verdien i D2 lik 1 ved å endre celle D2. Programmet finner altså løsningen på 1 = x2 − ln x.
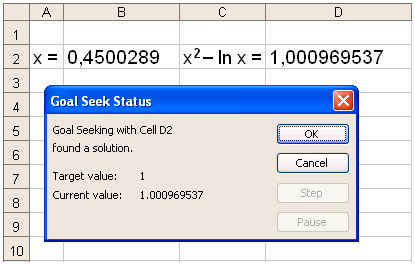
Vi får at x ≈ 0,45, og ser at svaret vi fant i eksempel 6 var ganske nøyaktig.
Prøv test 3 i Likninger III.
Husk å bruke sjekklisten for å få oversikt over hva du har gjort.