© 2008  Rasmus ehf    og Jóhann Ísak

Föll 2

  Kynning 2

Jafnstæð, oddstæð, átæk, eintæk og gagntæk föll

Myndirnar hér fyrir neðan sýna gröf fallanna f(x) og g(x).

Við skulum rifja upp hugtökin formengi (F_f) og varpmengi (V_f) en á myndinni t.v. er F_f = [1, 5] og V_f = [2, 4] en á myndinni t.h. er F_g = [1, 3] og V_g = [1, 4].

Fallið f(x) er stöðugt á uppleið í öllu formenginu, þ.e. fallgildin hækka með vaxandi x-gildi. Þegar svona háttar til er sagt að fallið sé vaxandi enda sveigir það hvergi niður á við í formenginu.

Myndin t.h. sýnir hins vegar fallið g(x) sem er minnkandi í formengi sínu.

Í framhaldi af þessu getum við skoðað fall sem er bæði minnkandi og vaxandi. Fallið f(x) = x² er t.d. minnkandi á bilinu á¬,0] og vaxandi á bilinu [0,®ñ eins og myndin hér fyrir neðan sýnir.

Fallið f(x) = x² er eins og kunnugt er samhverft um x-ásinn (samhverfuásinn er x = 0 eða y-ásinn). Föll sem þannig háttar til um nefnast jafnstæð föll (eða jöfn föll).

Oftast er einfalt að sjá á grafi hvort föll eru jafnstæð, en það má sannreyna með því að athuga hvort almennt gildir að f(–a) = f(a).

Sýnidæmi 1

Athugum hvort  er jafnstætt fall.

Byrjum á því að skoða grafið í grafískri reiknivél. Vélin sýnir grafið svona:

Þetta virðist vera jafnstætt fall en til þess að fullvissa okkur um það skulum við gera eftirfarandi prófun.

Fallið er jafnstætt.

Sýnidæmi 2

Athugum hvort fallið f(x) = 8(e^x – x – 1) er jafnstætt.

Grafið lítur svona út í grafískri reiknivél:

Grafið minnir á fleygboga og gæti fljótt á litið verið jafnstætt, en við skulum gera prófun.

   f(–a) = 8(e^–a – a – 1)

     f(a) = 8(e^a – a – 1)

Þetta tvennt er aðeins jafnt ef e^–a = e^a sem ber með sér að jafnan –a = a verður að gilda.

Jafnan –a = a hefur aðeins lausnina a = 0 þannig að (0, 0) er eini punkturinn á grafinu sem uppfyllir skilyrðið f(–x) = f(x) þannig að fallið er ekki jafnstætt.

Skoðum nú aðra gerð af samhverfum eða samhverfur um miðju hnitakerfisins. Gröf af þessari gerð eru þannig að ef við snúum þeim 180° um punktinn (0, 0) þá falla þau ofan í sjálft sig.  Dæmi um þetta er graf f(x) = x³.

Örvarnar á myndinni hér fyrir ofan sýna að ef við snúum grafi  f(x) = x³ í hálfhring um miðju hnitakerfisins þá fellur það ofan í sjálft sig. Föll af þessari gerð eru samhverf um (0, 0) og það gerist aðeins ef f(–x) = –f(x).

Föll með þessa eiginleika nefnast oddstæð (eða ójöfn).

Þetta getum við notað til þess að prófa hvort föll eru oddstæð.

Sýnidæmi 3

Athugum hvort fallið er oddstætt.

Skoðum grafið, t.d. í grafískri reiknivél.

Fallið virðist nokkuð greinilega oddstætt en við skulum ganga úr skugga um það með prófun.

Prófunin sýnir að f(–a) = –f(a) þannig að fallið er oddstætt.

Föll sem verða til við hliðrun á jafnstæðu falli eru samhverf um lóðrétta línu. Við þekkjum þetta frá gröfum annarrs stigs margliða, en þau eru öll fleygbogar með samhvefuás í miðjunni og má hugsa sér að þau hafi orðið til við hliðrun á fleygboga með topp- eða botnpunkt í (0, 0). Til þess að finna samhverfuásinn verðum við að finna hliðrunina miðað við x-ásinn. Þá reynum við að umrita fallið á formið f(x–a) + b þar sem f(x) er jafnstætt fall. Ef það er hægt þá er x = a samhverfuásinn.

Föll sem verða til við hliðrun á oddstæðu falli eru samhverf um tiltekinn punkt. Ef við getum umritað fallið á formið f(x–a) + b þar sem fallið f(x) er oddstætt þá er grafið y = f(x–a) + b samhverft um punktinn (a, b).

Sýnidæmi 4

Athugum hvort fallið er samhverft um lóðrétta línu eða punkt.

Grafísk reiknivél sýnir eftirfarandi graf.

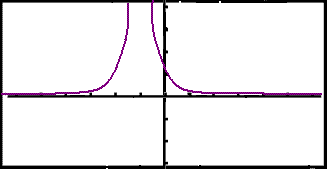Fallið virðist samhverft um lóðrðétta línu nálægt x = –1.

Við getum umritað fallið á eftirfarandi hátt:

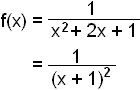
Fallið er greinilega hliðrun á fallinu um eina einingu til vinstri. Skoðum hvort g(x) er jafnstætt fall.

Fallið g(x) er greinilega jafnstætt og f(x) er myndað við hliðrun á g(x) um eina einingu t.v. 
Samhverfuás f(x) er x = –1.

Sýnidæmi 5

Athugum hvort fallið er samhverft um lóðrétta línu eða punkt.

Grafísk reiknivél sýnir eftirfarandi graf. 

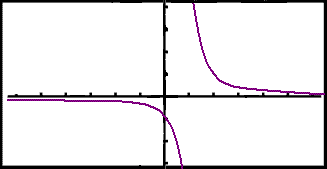Það hefur greinilega engan lóðréttan samhverfuás en gæti verið samhverft um punkt.

Fallið er greinilega hliðrun á fallinu um eina einingu til hægri. 

Við þurfum því að athuga hvort g(x) er oddstætt fall.

Fallið g(x) er oddstætt og samhverft um (0, 0). Fallið f(x) er myndað við hliðrun á g(x) um eina einingu t.h. þannig að f(x) er samhverft um punktinn (1, 0).

Hugsum okkur eitthvað talnamengi (t.d. R) og eitthvað tiltekið fall f. Ef fallið f hefur þann eiginleika að hafa allt talnamengið R sem varpmengi þannig að engin tala verði undanskilin þá er fallið sagt átækt.

Tökum sem dæmi fallið f(x) = x + 1 og veljum því formengið F_f = R og varpmengið V_f = R. Eins og kemur fram í gildistöflunni og á grafinu hér fyrir neðan þá eru allar tölur mögulegar sem útkomur úr formúlunni f(x) ef við getum valið inn í hana hvaða x-gildi sem er. Fallið f(x) = x + 1 er átækt.

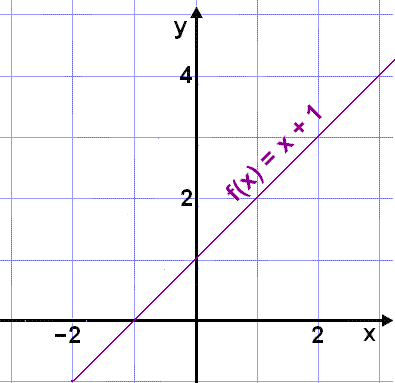	Í þessum dálki geta allar tölur birtst

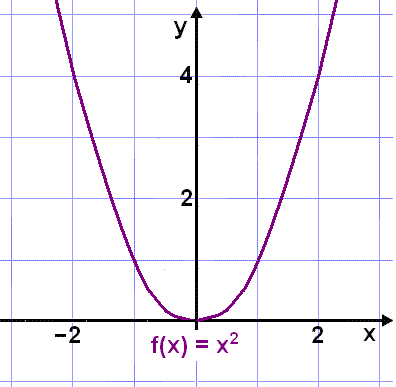
Dæmi um fall sem er ekki átækt í R er fallið g(x) = x². Gldistafla og grafið líta svona út.

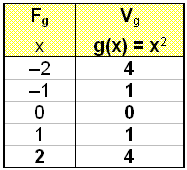	Í þessum dálki geta engar neikvæðar tölur birtst

Fallið g(x) = x² er ekki átækt vegna þess að engar neikvæðar útkomur eru mögulegar. Ef við hins vegar veljum formmengið F_g = R₊ og varpmengið V_g = R þá verður fallið g(x) = x² átækt. Þá dekka útkomur úr fallinu allar hugsanlegar tölur í varpmenginu.

Eins og nafngiftin varpmengi ber með sér þá eru föll stundum nefnd varpanir enda má líta svo á að föll varpi stökum úr formenginu yfir í varpmengið. Við höfum fyrst og fremst fjallað hér um föll sem varpa tölum úr R yfir í R eða úr hluta af R yfir á annan hluta af R. Ef við hugsum þetta almennt þá getum við litið á átæku vörpunina f úr A yfir í B á eftirfarandi hátt.

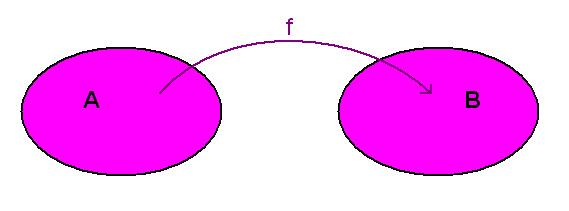
Við getum hugsað okkur að öll stök í B fái einhverja vörpun á sig.

Eftirfarandi mynd sýnir hins vegar fall sem er ekki átækt.

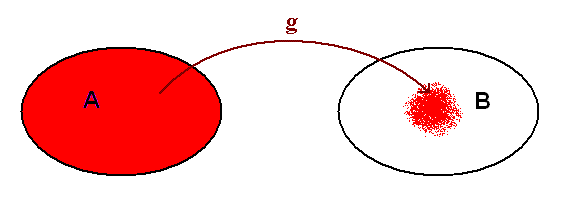
Vörpunin fyllir ekki upp í allt varpmengið B.

Við skulum nú skoða aðra gerð falla sem kallast eintæk föll. Þau eru þannig að það er sama hvaða mismunandi gildi úr formenginu (x-gildi) við veljum við fáum aldrei sama fallgildið oftar en tvisvar.

Þetta hefur það í för með sér að ef um samfellt rauntölufall er að ræða hlýtur það annað hvort að vera stöðugt vaxandi eða stöðugt minnkandi í formengi sínu. Lárétt lína getur þar af leiðandi aðeins skorið grafið á einum stað.

Sýnidæmi 6

Athugum hvort fallið er eintækt í formenginu á–2,®ñ.

Ef fallið er ekki eintækt þá ætti að vera hægt að finna mismunandi lausnir á jöfnunni .

Við sjáum hins vegar að eina lausnin er þegar x₁ = x₂  þannig að fallið f hlýtur að vera eintækt. Við sjáum það líka á grafinu í grafísku reiknivélinni sem reyndar sýnir allt grafið ekki bara efri hlutann eins og formengið á–2,®ñ segir til um.

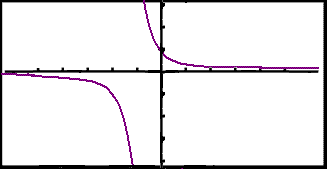Lárétt lína getur aðeins skorið þetta graf einu sinni.

Sýnidæmi 7

Athugum hvort föllin f(x) = x² og g(x) = x³ eru eintæk.

Nú er t.d. f(–1) = (–1)² = 1 = f(1) þannig að fallið f(x) er ekki eintækt.

Hins vegar gildir þetta sama ekki um fallið g(x) = x³ vegna þess að g(–1) = (–1)³ = –1 og g(1) = 1. Skoðum grafið í grafískri reiknivél.

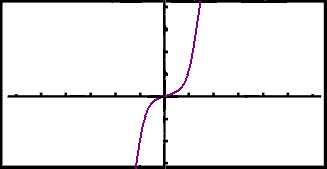Það er ljóst af grafinu að fallið er vaxandi í formengi sínu og lárétt lína getur aðeins skorið grafið á einum stað. Fallið g(x) er eintækt.

Föll sem eru bæði átæk og eintæk nefnast gagntæk. Fallið g(x) = x³ sem fjallað er um í sýnidæmi 7 hér fyrir ofan er gagntækt í öllu talnamengi rauntalna R. Það er eintækt vegna þess að grafið er samfellt frá y = –∞ upp í y = ∞. Til viðbótar er fallið stöugt vaxandi í öllu formenginu R þannig að það er eintækt og þar með gagntækt.

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í Föllum 2.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum